
The importance of caching in chess engines
My chess engine development has been on a small hiatus lately but I am by no means finished. There is much more work to be done and many topics I want to address. I really want to talk about Magic Bitboards and Transposition Tables. Both of those are rather heavy topics and I think they deserve a simpler introduction.Introduction
It's been a while since I have written one of these. The project has been on a bit of pause so that I can take a break and work on some other projects meanwhile. There are many topics I want to write about and the two at the top of the list are a closer look at bitboards and transposition tables. More specifically magic bitboards- a fantastic way to obtain moves for sliding pieces in an instant. Transposition tables allow storing and retrieving positions with their evaluations. Both of these topics are very important to computer chess as they have been very crucial building blocks to the insane strength engines have grown to over the decades.
They are also both heavily involved and deserve a lot of attention. To lay out the motivation and foundations might be too much for a single entry and since they both have some overlaps this entry will focus on caching as a way to ease into the topics.
What is caching and what is it good for?
Cache is a mechanism of storing data in memory for later retrieval. This is usually done for heavy computations where the result can be reused at a later time. One example would be your browser cache. When you access an entirely new web page you need to download everything from the server. However, when you navigate the website from one page to another a lot of data might not change - the style sheets used, the banner images, the site footer and many other resources. It is unfeasible to always download these things from the server with each request. The browser can actually save a lot of this in memory or disk and when loading a new page it can often forego re-downloading them and use the version previously obtained. Caching is used in many tech solutions. When performing a query against a SQL database there is a good chance that running it a second time the answer will be instantaneous if the data queried has not changed since.
We sometimes cache things ourselves. A good example would be basic multiplication. If you need to multiply any two numbers that are in the all familiar 10x10 multiplication table, there is a good chance that you are not actually multiplying anything in your head at all. You most likely have memorized the whole multiplication table for small numbers and know the answer immediately. We come across these simple multiplications often enough to have memorized them.
Remembering multiplication results has its obvious limitations. The numbers are infinite which prevents us from remembering ALL of the multiplications. So we still need to be able to do actual multiplication but knowing some results by memorization can simplify the actual calculations we do have to carry out. So caching is doing work once and then remembering the result for instant use later without repeating the actual work to obtain it. These are the basic principles of caching. There are certainly benefits to doing it and there are also limitations to what extent it can be done and where it can't be used at all.
Knight moves
With the basics covered let us move onto chess. While it is impossible to pre-calculate all the multiplications and store them for later use due to the numbers being infinite and honestly multiplication is so easy for a machine it just does not make sense to read a result from a multiplication table instead of doing the multiplication on the fly.
The chess board in contrast is finite it only contains 64 squares. So many calculations on a square can be done once in advance and reused. Let us look at knight moves on an empty board. It is a good example as knight moves are a little bit annoying to compute due to their peculiar move patterns.
In this example we will use a one-dimensional array representation of the board (the same principles apply to bitboards). If you need to refresh your memory on how the 1D board representation works, you can revisit the previous blog entry. We established a compass for all boards- a simple method on how to address adjacent squares from our central square:
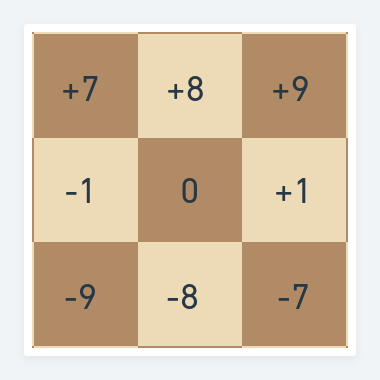
With the basic concept of a compass let us extend the idea to knight moves:
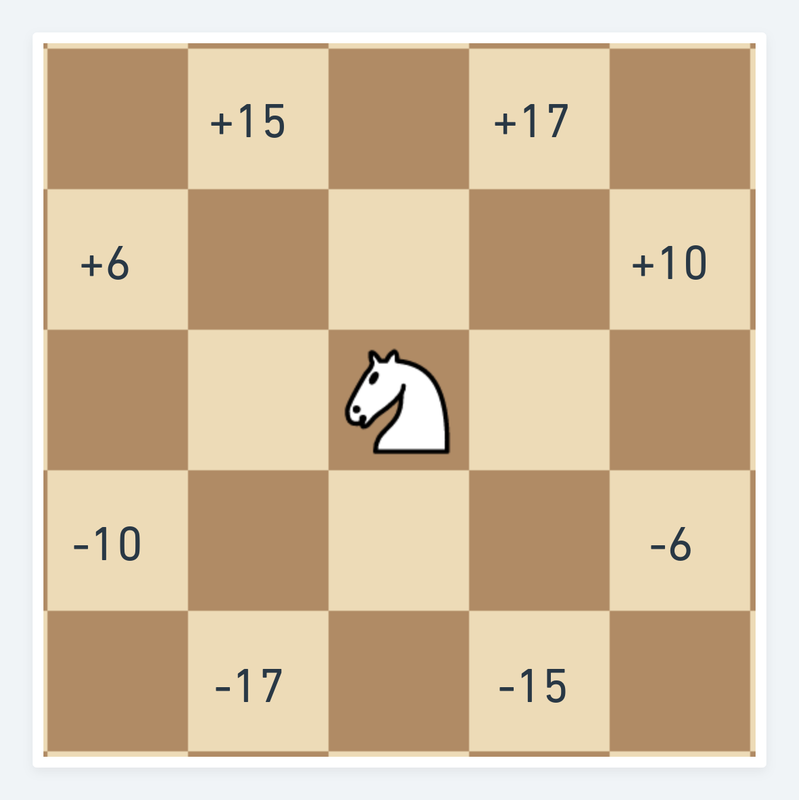
Using the compass above you can easily compute these values for example: +15 = 16 - 1 - moving two ranks up and one to the left.
This is a full description of all eight possible knight moves. Take all eight numbers and add the index of the source square and you will have the indexes of possible destination squares for the knight. The problems start when you consider knight moves close to the board edges. At the top and bottom we need to ensure that the knight doesn't fall off the board - the coordinates must be less than 64 and not negative. At both sides of the board we need to ensure that the knight doesn't wrap around the edges and doesn't jump to the opposite side of the board.
So for every of the eight moves you need to perform two independent checks to ensure the move is legal- the distance to left/right edge and the distance to top/bottom edge. For a modern computer it is not an issue to evaluate eight if-statements with two comparisons of basic arithmetic each. So why would you need to pre-calculate and store something so trivial?
If you think about it, it is actually not that trivial or, to be more precise, it can be further simplified. When programming a chess engine performance is the primary objective - you want your engine to play as good as possible. In this context performance is exchangeable with playing strength. The playing strength comes from various different areas of the engine. In the most simplified way these areas could be divided into two categories - how smart it is and how fast it is. Smart comes from the various algorithms it uses - good evaluation, sophisticated search techniques, etc... Speed simply defines how fast those algorithms run. So overall playing strength could be approximated with a empirical formula:
strength = smarts * speed
This is very well illustrated by the current top engines - Stockfish and Leela. Stockfish is a mostly classical engine and it is very fast - it evaluates an insane number of positions every second. Leela on the other hand is a Neural Network engine. It evaluates fewer positions but it does so much better- smarter. So to contrast the two: Stockfish gets it strength mainly from speed and Leela from being smarter. When you watch them battle each other their total playing strength ends up quite close.
Back to the knight example. We can not make the legal knight jumps any smarter we can only make sure we can calculate them faster. The knight move calculation from a given square is a very good candidate for caching due to obvious reason:
- The knight moves never change. They are the same for white and black. A knight can jump over pieces so its trajectory can not be blocked by other pieces on the board.
- The moves can be easily accessed from memory by using the square the knight resides on as a key. For example a knight on a1 will always have b3 and c2 as its possible destination squares etc...
- The calculations can be done once at the start of the program or even hard-coded in a static way and easily accessed for the rest of the game.
So a relatively simple function with the square as a parameter that has to perform the legality check of eight moves can be replaces with a pre-calculated array with the square as a key that returns a fixed array. The latter is clearly considerably simpler.
Optimizations usually come at a price and are the sum of trade-offs. What are the trade-offs here? And at what cost?
- Storing values in memory or even extra lines of code take up more memory. The price to pay here is laughably small. Even quite old machines will have zero impact on a few extra bytes in memory or a slightly larger executable file. While some hash tables can incur noticeable memory cost, in this case it is absolutely insignificant compared to the computational cost of calculating the moves on the fly.
- Complexity. You need to write a function that calculates the knight moves from a given square regardless if you want to cache or not. To store the results in memory you also need code that handles the data structures that hold the source-destination relationship. You need to write extra code that executes on program initialization to pre-calculate these values then store them etc... So it is inevitable that to cache knight moves you will need to write some extra code compared to just always calculating them on the fly by a single function call. Compared to the first point this is a more realistic price. It is time and effort that could be spent on other aspects of the program. Ultimately it is not rocket science and the benefits are significant enough to make it worthwhile.
Summarizing caching
We took a very simple problem and we simplified it even further at a very low cost. While this might look a bit comical on the surface - splitting hairs. It is more significant than you might at first realize. For strong engine play a lot of positions need to be evaluated every move. The number can range from thousands to millions per second for an approximate range. For each position we could potentially need to calculate the possible eight moves for each of our two knights but also for the opponent to detect checks on our king by opposing knights. While in isolation this might not make your engine much stronger, employing the same good practices across various areas can bring great compund improvement to the speed of your engine.
The next obvious example for caching would be to do the exact same for king moves. While king moves have a simpler pattern than knights they still are good candidates for pre-calculating and caching for the same reasons knight moves are.
Another less obvious area of caching can be pre-calculating the distances a bishop or a rook can slide on an empty board in a particular direction. So when one actually comes to generating those moves in a real position, it is no longer necessary to check if a sliding piece is about to hit the edge of the board - the distance that needs to be checked in a compass direction is pre-calculated and bound to the board coordinates.
In general if something can be calculated once and then recalled from memory it is probably a good idea to do so. In applications where performance is not crucial this might result in more code and over-engineering and creating more work for the programmer where the machine can be made to do the extra work simplicity at no significant cost. This is not the case for chess engines.
Conclusions
What I really wanted to talk about is magic bitboards and transposition tables. Both of them are optimizations that allow to reuse work done previously at a fraction of the computational cost. This is just a primer to ease into those advanced topics. I still hope I managed to lay out the motivation and basic principles of caching within a chess engine.
Magic bitboards
The next topic I will cover will be Magic bitboards. Magic is used in computer science in many different contexts. Sometimes complicated or obscure code that works is just dismissed as magic. This is a bad programming practice either by the person writing incoherent code or the reader not putting in the necessary effort to understand it. Sometimes variables and values in code that are used for a specific purpose without proper documentation is referred to as a magic value. It's just there and probably means something to someone. In our case we will use logical code and in principle well defined values that serve a clear purpose. The problem is that to find those values often the best approach is to simply try random guesses until they magically work.
What magic bitboards do is to pre-calculate moves for sliding pieces. This is trivial on an empty board but once you start adding opposing and friendly pieces their movement paths can be blocked. So in practice it impossible to use pre-calculated look up tables for bishops and rooks because of the impossibly many positions that can arise in a chess game.... unless you use magic.
(Disclaimer: Not actual magic. Just some smart maths and hashing)
Transposition Table
When I rewrote my code to a tree-less search function I reduced the memory usage of my engine to practically zero. However, when you observe any competent chess program in a task manager you will see it actually consumes a significant amount of memory. This memory is usually all used up by the transposition table. A transposition in chess is reaching the same position by a different order of moves.
For example as white you could play the English opening: 1. c4 Nf6 and continue with the variation 2. d4
This can also be reached by opening with 1. d4 Nf6 2. c4 1 - 0. Black Resigns! Ouch! Too soon maybe?
If while calculating a variation, we reach the same position but with a different move order leading up to it we can stop our calculation right there if we can recall the evaluation of the previous position reached by different moves. Transposition tables are data structures that allow us to store positions in a game for later use. They can have the exact evaluation attached to them or alpha / beta bounds in case the branch was abandoned due to a cutoff from alphabeta algorithm. The benefits of using them are obvious and they become even more pronounced in the endgame where they allow the engine to reach much higher depths of analysis due to the fewer number of pieces leading to more transpositions. I have had my battles with them already but this announcing to write a in-depth blog about them leaves me with no option than to finally fix them and implement them properly.
You may also like
 likeawizard
likeawizardTofiks v1.1.0
It's been a while since v1.0.0 but we got there and we will keep going. After all a good dog require… likeawizard
likeawizardThe highly frustrating side of chess engine development.
While chess programming has been my top hobby and passion over the last two years. At times it comes… likeawizard
likeawizardReview of different board representations in computer chess.
Over the months of coding my engine I have gone through several implementations of the way the board… ambrona
ambrona