Review of different board representations in computer chess.

A brief history of chess board notation

Currently the most common board representation is the algebraic one. We have ranks starting from 1 to 8 going upwards and files from A to H going from left to right from white's perspective. To address a square we would first refer to the file and then the rank. For example a1 is the bottom left square from white's perspective and h8 the top right respectively. Obvious stuff.

This is by no means unique and if you find an older chess book or article in English or French or a select few other languages you will often see files being named after the piece that occupies it at the start of the game. This is called the Descriptive notation.

So for example the h1 in algebraic notation becomes QR1 and is pronounced 'Queen's Rook one' in the descriptive notation. And h8 KR8 - King's Rook eight. In some instances even the ranks are flipped back and forth depending on the perspective of black or white. So QR1 from the white perspective can be the same as QR8 from the black perspective.

Another alternative was used by Correspondence Chess - chess played over mail (electronic or physical) and was the standard for ICCF - International Correspondence Chess Federation. In that context files were addressed not by letters 'a' through 'h' but the same as ranks - numbers: 1 through 8. 1 being the a-file and 8 h-file

So again the all familiar a1 square in this notation becomes 11 and h8 becomes 88.

If you have seen some content of GM Simon Williams you will know he likes to use names for pawns depending on their file. So "Pushing Harry" translates to "pushing the h-pawn".

I am sure there are/were others. The point is we are all talking about the same game of chess. The same rules, the same games, the same moves but using different languages. Only relatively recently has the algebraic notation become the one golden standard used everywhere and by everyone. There is no indisputably best notation. It is all a matter of habit. Very much like the difference in metric vs imperial systems and Celsius vs Fahrenheit.

When developing a chess engine the choice of the board representation is one of the core decisions you'd have to make. You will spend a lot of code and time manipulating pieces, generating moves for pieces, determining if a king is in check or evaluating material count and quality. No matter what you do, you will have to interact with the board a lot. So the choice of board representation can make certain aspects easier and others harder.

Two-dimensional [8][8]array

Ask any software developer not familiar with chess programming what would be a good data structure to represent a board and my guess would be that the majority would suggest a two dimensional array of integer, string or maybe even some user defined type to hold a piece at the indices of the board array. This is exactly what I came up with in my first implementation as well.

This is the most intuitive choice as it closely mimics how we are used to talk about chess and how we see the board. There are some advantages to this choice.
(Spoilers: they are few and the disadvantages heavily out-weight them)

It is certainly helpful to use a very intuitive representation of the board. When you write a program you translate your thoughts and ideas into code. So having a straightforward transformation of your existing ideas into code can be helpful. If you are new to chess programming and want to learn the basics and figure out things yourself it certainly is a solid choice.

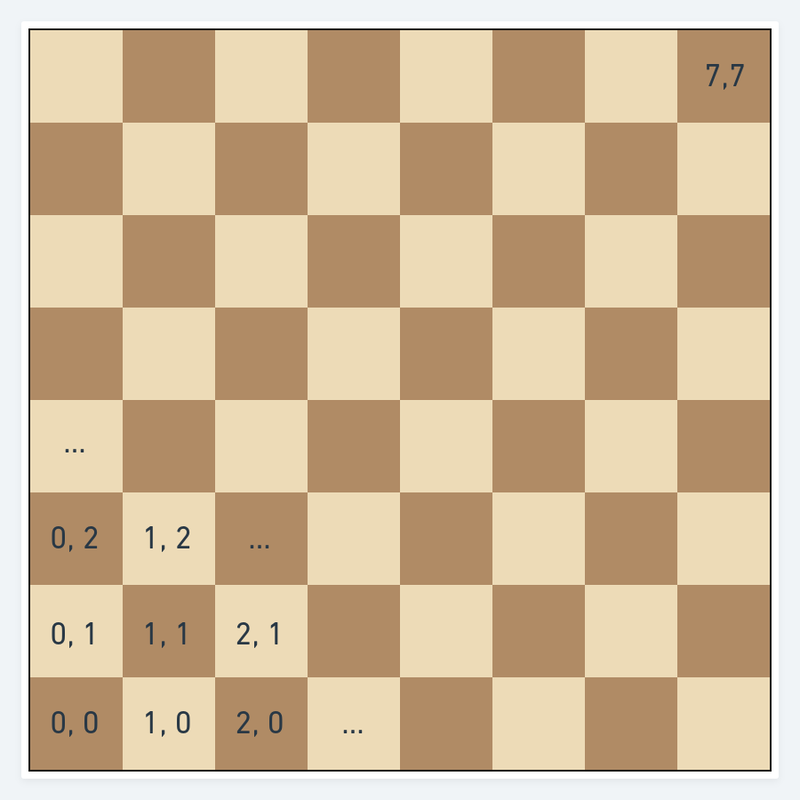
Visualization of a board represented by a 8 by 8 array. I am using the widely accepted convention that indexing starts at 0 and not 1 as can be seen on a physical board.

Addressing individual squares and navigating the board is very straightforward. A square can be addressed very much in the same way as in algebraic notation Board[File][Rank]. Say Board[0][0] would be the a1 square and Board[7][7] - h8. Then moving from one square to any of its neighbors is also very intuitive - you increase the rank to move forward, decrease it to move back. Increase the file to move right and decrease it to move left. When you have reached the maximum or minimum rank or file you know that you can move no further in that direction.

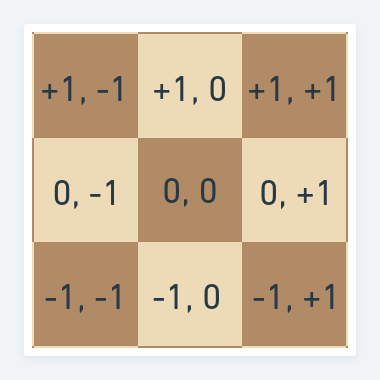
A compass as seen in the 2-dimensional approach

This is where the advantages end. The disadvantage of this approach is talking about individual squares. To refer to a single square you will always need two values - rank and file. To scan the whole board you will also need two nested loops - one to go through the ranks and one for the files.

for file := 0; file < 8; file++ {
    for rank := 0; rank < 8; rank++ {
        Board[file][rank]
    }
}    

You could of course define a coordinate object as a tuple to contain both values in one variable but that adds a layer of complexity in itself. When talking about moves it becomes twice the trouble. Now you need to keep track of four values- starting file, staring rank, destination file and destination rank. It ends up with a lot of code. Lots of values and many opportunities to make a typo in the wall of text that your code will become.

One-dimensional [64]array

This I believe is a good improvement of the two dimensional array. Instead of talking about squares in terms of files and ranks we simply use a flat one dimensional array to address each square by a single number. So our a1 square would be addressed by Board[0] and h8 Board[63].

Let us first address the loss of our intuitive addressing of squares. It was quite obvious in the previous case that Board[3][4] would translate to the square d5. It is quite easy to translate 'd' - the fourth file into the index 3 and the file 5 to the index 4. But how can we translate the square d5 (3,4) to the index for our one-dimensional array. The math is not complicated. You multiply the rank by 8 and add the file. This gives us 4*8 + 3 = 35. So Board[3][4] is the same as Board[35]. While the math is simple I had to double check my working. This can sound a bit daunting but "surprisingly" computers have little issues doing basic arithmetic and once you get your code set up, you will not worry about these details.

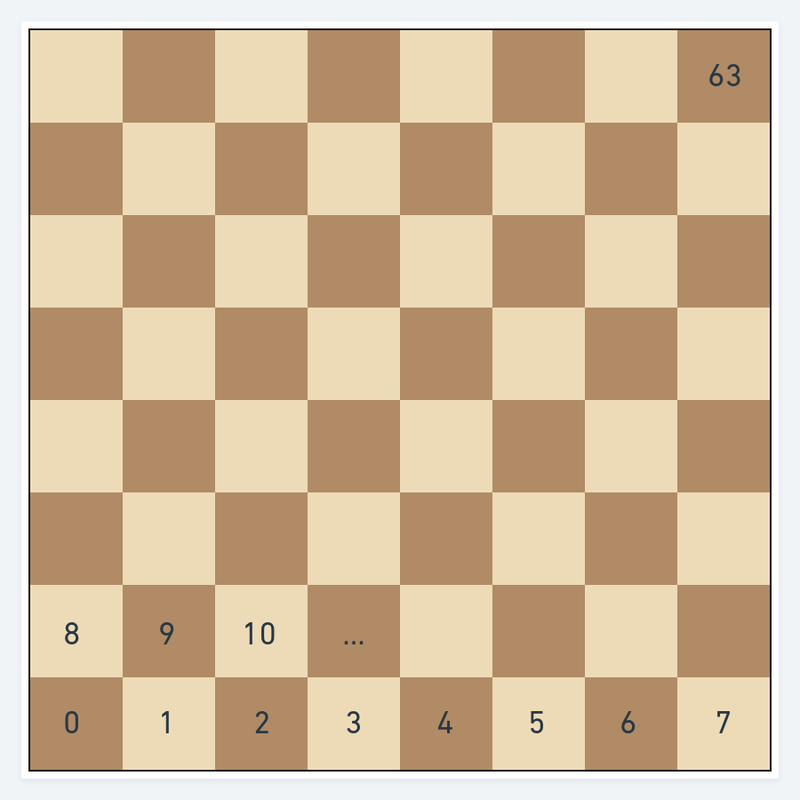
While the 64 element array has no rows and is simply a flat list, we can imagine that every eight squares it wraps into a new row

Another problem is moving pieces around on the board. It was very convenient in the two dimensional array - increment and decrement your rank and file indices to move about. How does this translate to the one dimensional array? Actually the same way we calculated the square d5 or any other square: square = rank*8 + file. So to move forward we have to add 8, backwards subtract 8, left subtract one and right add one.

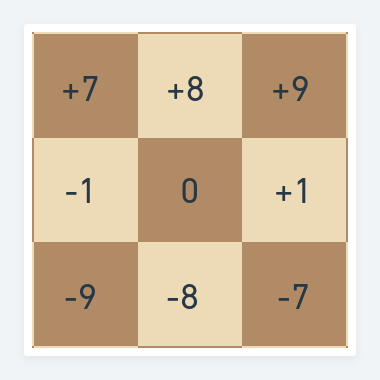
A compass in the 1-dimensional array. Left and right is still similar to the 2D array. Moving up or down requires the addition/subtraction of 8. And all other directions are the sum or difference of the existing directions.

You can take some time and convince yourself that moving around in these flat 64 squares you are actually moving about in a 2D space. Furthermore, when coding these arbitrary shifts of +9 or -7 being North-East or South-East in time it will become second nature to you. You will quickly become very comfortable reading and writing code in this coordinate system.

Don't get too comfortable though... Let's look at a square on the edge of the board in this representation and draw our compass there.

Ooops! That doesn't look correct.

What has happened here? Well you can convince yourself that moving right is simply indexing the array at +1. The computer doesn't care about our imaginary files and ranks. When moving one square to the right from the h-file we end up on the a-file but one rank up. A similar thing would happen attempting to move left on the a-file. What's even worse in the above picture attempting to move up and right we end up with an index of 64 our of our maximum of 63. Not only have we tried to move off the board but our program will crash as we are accessing an index that is out of bounds.

The solution - make conditional checks and ensure that any movement on the board does not wrap around the edges of the board. This behavior will certainly sprinkle your code with bugs initially. But after putting all the necessary checks in place you can forget about it and your pieces will move sensibly and not crash your engine.

What have we gained from moving from the 2D eight by eight approach to the 1D 64 square approach? Some simplicity - a square can be addressed by a single variable and a move by just two - from and to. Scanning all the squares on the board now only requires a single loop:

for square = 0; square < 64; square++ {
    Board[square]
}

It certainly needed some extra care to ensure we don't wrap around the edges but the simpler data structures and fewer variables associated with it will make our code smaller and in many cases more universal. It will eventually work faster and it with time be more easy to read and have less spots for bugs to creep in.

This is a good spot to reflect on what we covered so far. We started with the natural 2D approach - something very familiar and intuitive. Life was simple back then. It wasn't much but it was honest work. We upgraded from 2D to 1D. This became somewhat more obscure and was a move away from familiarity. As a trade off we got simpler and smaller code and some performance gains. We didn't do anything wrong in either approach but we have to realize the trade-offs made in that transition.

• Two dimensional array approach
  • Intuitive
  • Simple logic to implement
  • Very verbose
  • Potentially slow
• One dimensional array approach
  • The basic ideas are not as intuitive
  • Needs more caution and checks
  • Smaller and more universal code
  • Improved performance

Writing a chess program is not easy and you will encounter many difficult challenges. There is no magic way to make them all disappear. The choices you make end up being trade-offs between different areas: Easy vs difficult. Fast vs Slow. Compact vs Verbose.

Bitboards - unsigned 64-bit integers

This is the big one. This is what most of the highly competitive chess programs have been using for decades and still use today. I already covered bitboards in an earlier blog post. However, back then I had only read about them on the Chess Programming Wiki and not implemented them myself to really be able to talk with any expertise. But even then I suspected that it is the way to go. I first refactored my board from 2D to 1D (We will see that the 1D approach shares many things with bitboards) and I also started to encode things like castling rights and moves inside integer values using their underlying bits. Just to make gradual improvements and become more familiar with bit twiddling so I am in a position to implement them in my program.

So what are bitboards exactly? It's a 64-bit integer or it could be any other data type with the fixed length of 64 bits. Unsigned integers are the most natural choice with their properties and operations. What exactly does 64-bit mean? The native language of computers is ones and zeroes. So all numeric values eventually are translated into binary and 64-bit simply means that these are values that can be described by a combination of 64 ones and zeroes. I think by now I must have mentioned the number 64 enough times for you to see the connection with the 64 squares on the chess board and also the 1D array representation.

So a bitboard represents a chess position by a number that is 64 bits long where the ones are squares occupied by pieces and 0 empty squares. Let's look at an example for clarity.

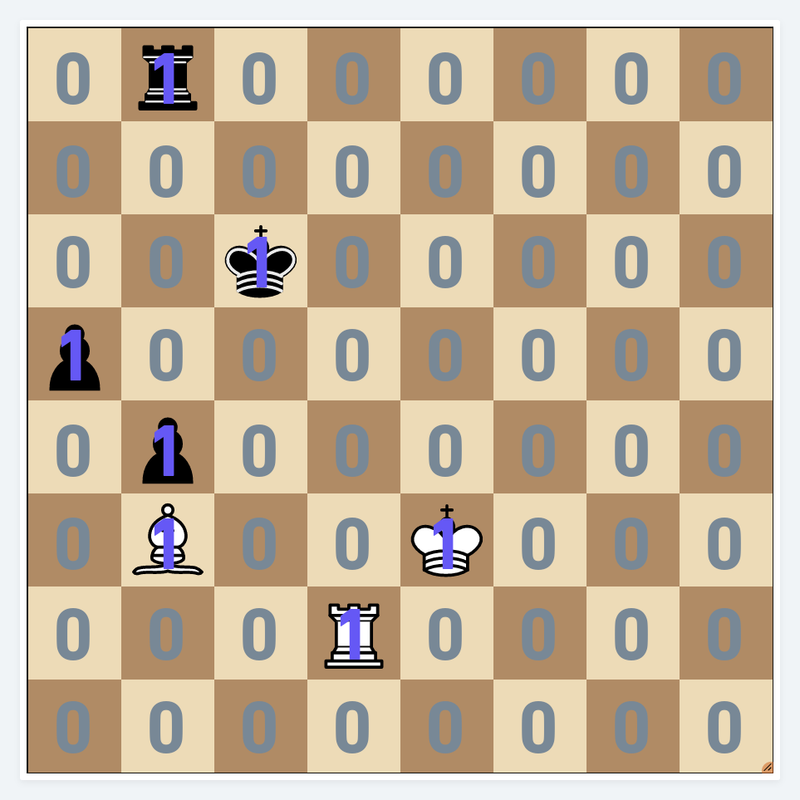
Position with pieces over-layed with high-bits and low-bits to indicate presence of pieces

Let's encode the graphical representation of the bitboard into the form it is actually stored. Let the a1 square be the Least Significant Bit (LSB) - the last digit in our number and the h8 square the Most Significant Bit (MSB) - the first digit in our number.

To encode the position into a number we will start from the top right, move left and down and record a 0 when the square is empty and 1 when it is occupied by a piece.

0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 0 1 0
0 0 0 1 0 0 1 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0

The result will ends up being mirrored horizontally due to our choice of the start and end squares and the order we move down the ranks. This is not a problem but you need to be consistent in the encoding and decoding.

Now let's put all the rows together starting from the top row and adding each next row at the end of it.
0000 0010 0000 0000 0000 0100 0000 0001 0000 0010 0001 0010 0000 1000 0000 0000

If I have not made any mistakes this is the occupied squares bitboard of our position. Often binary numbers are denoted with a '0b' prefix to distinguish between decimal 1000 (one thousand) and the binary 0b1000 which is 8 in decimal. So our binary number would look like this:

0b0000001000000000000001000000000100000010000100100000100000000000

We can convert this value to decimal by a variety of tools or pen and paper and the number comes out as:
144'119'590'452'070'400. This is 144 Quadrillion 119 Trillion 590 Billion.... Whatever! Nobody cares. We're here for the ones and zeroes and the numeric values have no meaning and utility to us.

If you've been paying close attention you might have an issue that was not addressed. In our approach we determined by 1's and 0's which squares are occupied. However, a 1 doesn't tell us whether it is a white bishop or a black king. That is true and is certainly a problem. The solution is to keep separate bitboards for different piece types. In fact you need 12 bitboards - one for white pawns, black pawns, white bishops, black bishops, white rooks and so forth... You can then combine these bitboards in more general sets - all pieces, all white pieces and all black pieces.

When we looked at the 2D and 1D arrays we also had a look at the compass - moving about to adjacent squares. Let's look at the compass for bitboards.

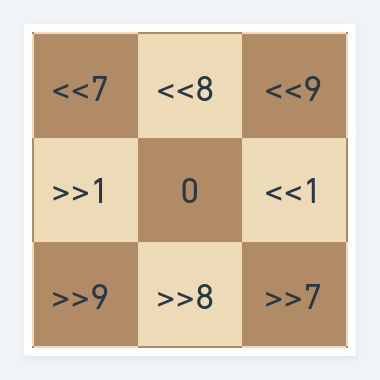
This should look very similar to the compass for the 1D array but instead of '+' and '-' we have '<<' and '>>'. These are bit shift operators. They take a number and shift all bits within it to the left << or right >> by the specified amount. A quick example:

0010 << 1 = 0100
0010 << 2 = 1000
0010 >> 1 = 0001
0010 >> 2 = 0000

It's interesting to note how in the last operation shifting the bits by two to the right the 1 at position 2 simply fell off. This is actually a really nice property. When moving about the array we had to be very careful that when adding or subtracting from the array index we still remained in the bounds or else we would encounter a nasty crash of our program. Here we do not have to worry - move too far and you fall of the board. While this sounds scary, in most cases it is not an issue as falling of the board on either the right or left simply prunes illegal squares and moves without any additional checks being necessary.
Checks at either side of the board are still needed to ensure pieces don't teleport from the h-file to the a-file.

While bitboards are great to represent squares occupied by pieces on the board, they can do much more. Bitboards are also used to generate moves. You can create a bitboard with all the bits that are legal destinations of a piece.

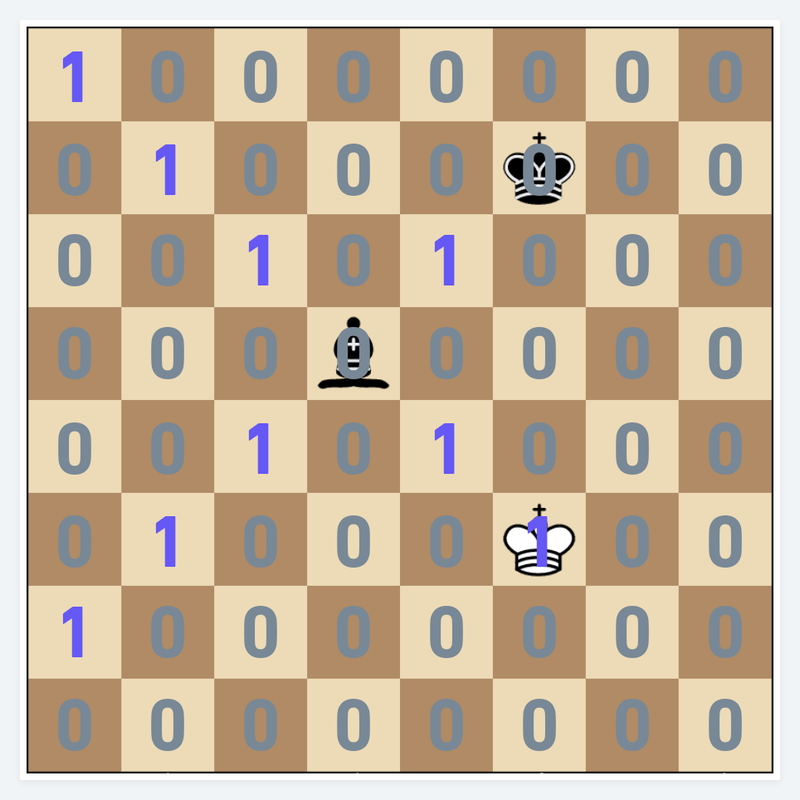
A bitboard of all the legal destination squares of the black bishop. The bitboard tells us that the bishop could capture the white king, which is illegal but it is simply in this case indicating that white's king is under attack and thus in check.

Bitboards usually are manipulated by bitwise operators such as the << and >> operators but there are many more. Which allow to perform many different actions or tests - combining move square bitboards with bitboards containing friendly and or opposing pieces can tell us if a move isn't blocked by a friendly piece or if a move is a capture of an enemy piece. It allows us to determine if a king is in check or whether a piece occupies certain squares of interest. When you start reading about bitwise operations you end up with a lot of mathematical set-theory lingo - unions, intersections, compliments. Fascinating and very useful stuff but way beyond the scope of this article.

Bitboards can seem complicated and they certainly are. Many modern programming tech stacks rarely require the developer to interact with the underlying bits. So becoming fluent in bit operations and various patters involving them can take some time. The rewards of doing so in the context of chess programming is invaluable.

What does really set bitboards appart from the 2D and 1D array representations? I think the most significant change is the way we can talk about chess. In the array representation we always had to lookup individual squares by an index and only by looking at the specific squares and the piece that occupies the square in isolation could we formulate concepts about the game. With bitboards we have a very natural way of talking about a set of pieces and squares without explicitly addressing the individual squares in the set. While surprisingly not adding much in complexity of talking about individual squares themselves.

I made a short list comparing 1D arrays to 2D arrays and I will do the same for bitboards.

• Very obfuscated to the uninitiated with a relatively steep learning curve.
• Less caution required as manipulating 1D arrays.
• Compact encoding and language to formulate various concepts.
• Simplicity in talking about individual pieces/squares or a set of them.
• Very efficient code. Ability to pre-calculate a lot of reusable data for impressive performance gains.
• Bitwise operations are much faster than iterating over array elements
• Needs separate variables for each piece type and more care when accessing them.

Summary

We had a look at three major board representations used in chess programming. There are some others too but they mostly are variations or combinations of these three. And they all come with their own advantages and disadvantages. What I failed to mention so far that the 1D and 2D arrays and the bitboard representations fall into two distinct groups of board representations. In the array variants we focused on the board then addressed each square and looked what it contained. This is a square-centric representation. With bit boards we had 12 distinct variables for each piece type that contained information on what squares they reside on. This is a piece-centric representation. It's again a minor distinction and does the same thing but various operations can be more natural in one and awkward in the other.

In the case that you are considering building your own chess engine and have come across this post, what board representation should you use?

In my opinion the bitboard approach is by far the best. My code is much cleaner. The statements and evaluations I make are much clearer and concise. However, if you are not proficient with bit-twiddling already you will have a hard time implementing them. You can find various sources and tutorials how to do it. Blindly following them you might even succeed but copying code without understanding will severely limit you when trying to expand on those ideas or fix bugs.

That is why I would strongly suggest to use a 2D implementation of the board for your first project. Everything will be easy to understand. You should be able to achieve most things on your own without much assistance and be confident about your work and focus on and learn other things like various search algorithms and building an evaluation function on top of it.

With time you might notice how cumbersome the 2D representation can be. In that case you should already have enough experience under your belt converting ranks and files into squares and back that you should not have much difficulty refactoring your code into 1D array. You will again need some time to familiarize yourself with the bizarre looking directional compass and all the wrapping issues.

And sooner or later you can again refactor the code from 1D array to bitboards. The many similarities between them should give you enough experience to code with confidence.

This is the exact route I took and thus the advice is very personal. I probably could have skipped the 2D array route and jump right into the 1D representation but I would have missed out on many lessons learnt.

Pick your own poison and make it work for you.