Vampires in Chess

Have you ever wondered how many legal positions exist in chess? Unfortunately, mankind is not ready to answer this eccentric question, although some estimations indicate that this number is comparable to the number of water molecules on Earth.

However, there is a more reasonable target that we could aim for: is the number of legal positions even or odd? It turns out there exists a very convenient way of grouping positions in pairs, by pairing each position with its mirror image. Thus, could not we conclude that the number of legal positions is even? Not so quickly. There exist legal positions whose mirror image is illegal. Such positions without a mirror image are known as vampires, a fun term coined by Andrew Buchanan, who has studied this thrilling topic for several years and who introduced me to it.

Mirror image of a position

Legal positions

First, let us clarify that a position is a configuration of pieces on the board (a diagram) together with the information of whose turn it is and what castling/en-passant rights are enabled. A position is said to be legal if it can be reached in an actual game.

The most promising attempt of pairing positions is the following definition of mirror images. (Other efforts fall short, e.g., pairing positions with the same diagram and different turn leads to problems with checks, or a diagram reflection with respect to the vertical axis leads to castling issues, etc.)

Definition of mirror image

The mirror image of a position is the position obtained after reflecting the board configuration with respect to the horizontal axis in the center of the board, inverting the color of all pieces and inverting the turn (castling/en-passant rights are preserved, reflected).

As an example, consider the starting position of the Spanish Opening and its mirror image, which is legal: it can be reached after e.g. 1. e3 e5 2. e4 Nf6 3. Nc3 Bb4. Note how we have moved the pawn to e4 in two steps in order to "lose a tempo".

Starting position of the Spanish Opening (left) and its mirror image (right)

Vampires exist

As we have anticipated, there exist legal positions with an illegal mirror image. In the rest of this post, I would like to help you discover that vampires exist by guiding you on how to find one. For that, we will leverage the following result.

Every vampire comes from a vampire

Exactly. Just as one would expect, vampires do not appear from thin air, they come from another "infected" individual.

Formally, what this means is that all preceding positions to a vampiric position are vampires. In other words, if we make a retraction on a vampire, we reach another vampire.

Proving this fact is not hard. Observe that by making a legal move on a non-vampiric position, we always reach a non-vampiric position. This is because the former position has a legal mirror image where we can make the analogous mirror move which leads to the (legal) mirror position that we wanted.

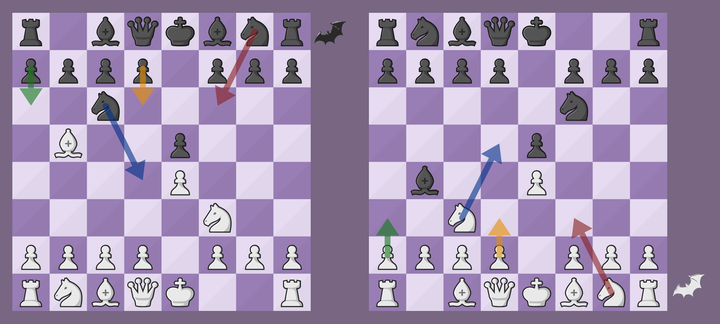
Every legal move in a position has a corresponding move in its mirror image

Can you now find a vampire?

If every vampire comes from a vampire and under the assumption that vampires exist. Would you be able to find one? In other words, there are no vampires in the tree of variations that starts in a non-vampiric position. If vampires exist...

The starting position must be a vampire! And, indeed, it is. If it were not a vampire, vampires would not exist. We can consider it the Head Vampire.

But why is the starting position a vampire?

The mirror image of the starting position is the same position with the turn inverted (Black to move). Such a position is in fact illegal because knights can only make even cycles, this makes it impossible to grant the turn to Black. In fact, all vampires are based on a parity argument of this kind.

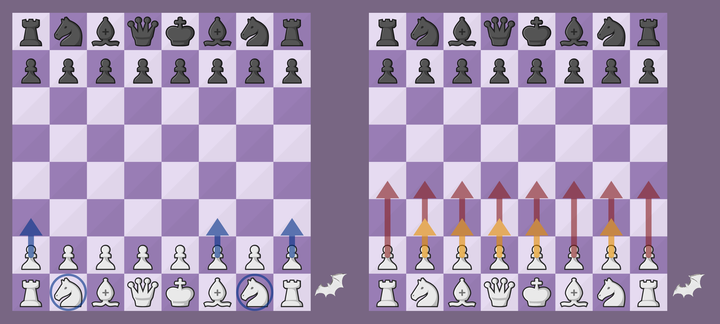
Only 1. a3, 1. f3, 1. h3 or knight moves preserve the parity invariant in the starting position

Challenge for the reader

I invite you (in the same way Andrew invited me) to find a vampire where en-passant is possible.

1. First, realize how hard it is to get a pawn advance without losing the parity invariant (a double pawn-push, e.g., loses the invariant because it allows for "triangulation", i.e. the pawn can push in two steps in the mirror image).
2. Then, find a way to get to the 5th rank on a vampire.
3. Now simply make a double pawn-push next to the pawn on the 5th rank. The en-passant flag will force the pawn to also push in one go in the mirror image, so you are good.

Happy Halloween and good luck!