Science of Chess - Problem Solving or Pattern Recognition?

In my last post about the Science of Chess, I talked a little bit about the possible pitfalls of focusing chess research on GMs and other titled players rather than including players of widely varying playing strength. Part of my rationale for being careful about basing our conclusions about chess and cognitive processes on high-level players was that it could be the case that extreme experts may use very different mechanisms to approach the same problem (a tricky chess position) than a more average player. The idea is that if we only look at the absolute best players, we may not be able to learn much about what's going on in the mind of most players when they consider what move to make, or how to formulate a plan during a game. What are you doing when you play chess? Yes - you.

Here, I'd like to highlight a study I read recently that has a lot of neat stuff in it, including what I think are some unique insights into aspects of cognition that don't always draw as much attention as others when cognitive scientists (and chess players) think about how the game is played. In particular, I've found quite a lot of chess research that proceeds from the assumption that pattern recognition in various guises is specifically important to playing chess well. My guess is that a lot of my readers have heard advice about building up pattern recognition via focused training on tactics (drill those puzzles!) but is that really the cognitive heart of the game? Unterrainer et al.'s (2006) paper provides some nice evidence that other aspects of cognition likely play a substantial role, too, and offers some surprisingly stark data points that suggest a quite specific hypotheses about cognitive processes chess entails.

How do you look for cognitive differences as a function of playing strength?

The overall design of this study is not so far off a previous paper I wrote about in my post about spatial cognition abilities in chess players. Like that study (Waters et al., 2002), this one focuses on determining how performance varies as a function of chess playing ability across some standard neuropsychological tests that are meant to serve as ways to operationalize some specific visual or cognitive abilities. Compared to that previous paper, however, this one also includes some different design choices that I was really excited about. First of all, rather than look for correlations across a range of player ratings, in this study the comparisons we will be interested in are between chess players and non-players. By itself, this isn't especially amazing - I mean, it's a perfectly fine choice, just nothing all that unheard of. What I liked, though, was that chess players meant a group of 25 individuals with ratings between ~1250 and 2100 ELO. That is a neat range to see! We're not talking exclusively about extreme experts - your humble NDpatzer might even make it into this sample, after all. It's also a pretty wide range of ability that the researchers will be treating as more or less just a source of noise/variability in the data. That is, the fact that a 1250 player likely differs a lot from a 2100 player in terms of chess ability may also mean that they'll differ from one another by a great deal in some other task. Que sera, sera - we'll just have to see how the statistical tests shake out.

The other thing that I thought was particularly neat about this study was that there isn't any chess in it! You may wonder why I (a chess blogger) was so pleased to see a cognitive study about the nature of chess playing that didn't include a chess task. For me, the interesting thing about this decision is that there is converging evidence from a number of cognitive science papers that playing chess makes you good at...well...playing chess. And look, that's fine - chess may turn out to be very domain-specific and if that's the way it is, that's what we'll find out. What I liked about this design, however, was the commitment to sort of side-stepping that obvious difference between players of different strength and focusing on standardized measures of cognitive ability without getting the chessboard involved. This gives us the chance (but no guarantee) of identifying more broadly applicable cognitive processes that play a key role in chess. So: What are these neuropsychological tests?

I'll start with the ones that did not lead to any significant differences between the groups. These are a nice line-up of cognitive assessments meant to cover a number of processes that might contribute to effective chess play and are all examples of tests that I teach my students about in my Neuropsychology course - at this point they feel kind of like old friends. Without further ado:

The Standard Progressive Matrices test (SPM)

If you've ever taken an IQ test (an online one or a formal assessment), you have probably seen these before. Each item in this test presents the participant with an array of shapes, with variation across the rows and columns of the array defined by some rule by which the patterns are transformed. That rule may have to do with shapes, numerosity, patterns made by light and dark regions in the form, or other visual properties of the items. This assessment is frequently used as a proxy of fluid intelligence.

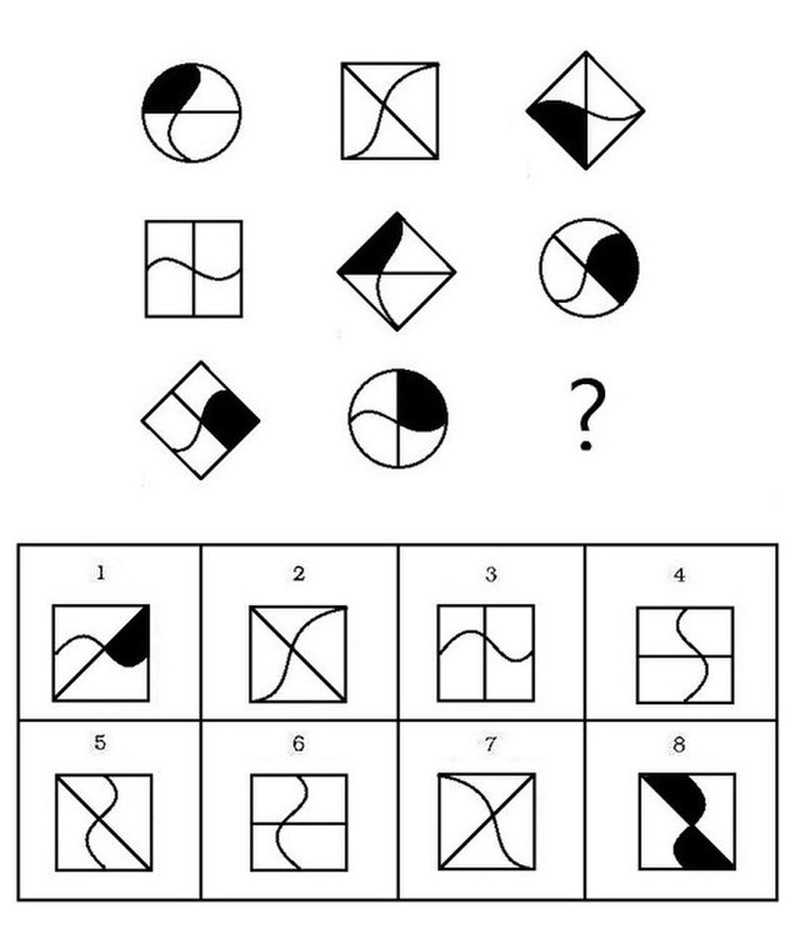
Which of these options should go in the empty space above? Wles05, CC BY-SA 4.0 <https://creativecommons.org/licenses/by-sa/4.0>, via Wikimedia Commons

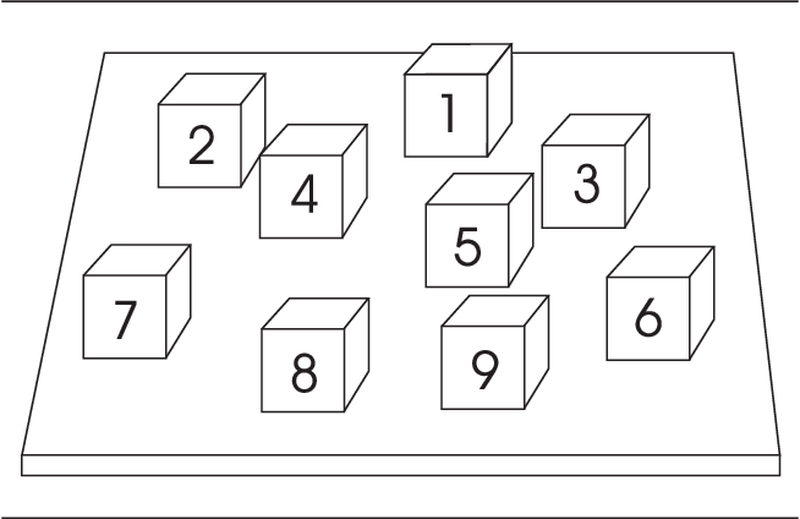
The Corsi block-tapping test

We have one of these in my department and I just love the physical apparatus for this one. This is an array of cubes set into a plastic surface in a pseudo-random arrangement (this means they are sort of jittered around rather than being lined up in neat rows and columns), each cube bearing the order in which it is to be tapped. The catch of, course, is that the person administering the test gets to see this order while they tap the blocks in front of the participant, but the participant then has to try and recreate that order without the aid of the numbers. In the "backward" version of the task, the participant is supposed to recreate the order in reverse.

A Verbal Working Memory Digit Span task

Pretty much what it sounds like and no neat-o testing apparatus to show off. The experimenter speaks a sequence of numbers to you at a steady pace and you are asked to either repeat it in the same order, or to repeat it in backwards order.

Like I said, none of these turned out to differ between our two groups of participants, which by itself is kind of interesting. The Corsi task is intended to be an index of visuospatial memory, which you could imagine might be very relevant to playing chess. On the other hand, if you think chess players might do a lot of more verbal processing to work with sequences of moves (e.g., e4-e5-Nf3-Nc6-d4-capturescaptures) then you might expect some differences in the verbal working memory task instead. The absence of differences in these cases (as well as in that fluid intelligence assessment) are at least a little suggestive of what doesn't turn out to matter so consistently.

Ah, but now on to the fun part...

The Tower of London task

I'm going to spend a little time talking through how this task works because interpreting the results of the study depends on knowing exactly what people were expected to do in this assessment. The Tower of London task is a standardized neuropsychological test that is intended to index abilities like planning, goal monitoring, and linking action plans to outcomes. It looks a lot like a common puzzle that you may have seen before: The Tower of Hanoi.

Image by Ævar Arnfjörð Bjarmason.

In the Tower of Hanoi puzzle, your goal is to move the discs from one post to another, replicating the original largest-to-smallest stacking order, subject to the following rules: (1) You cannot move a disc that has another disc on it, (2) You cannot put a disc on top of one that is smaller. I kind of love this puzzle because it was the thing that finally got me to understand mathematical induction, which in turn helped me see how to solve it. I'll spare you that revelation in favor of telling you how the Tower of London task (our actual assessment of planning in this study) differs from this puzzle.

Image credit: Gcappellotto, CC BY-SA 3.0 <https://creativecommons.org/licenses/by-sa/3.0>, via Wikimedia Commons

In the Tower of London (ToL) task you are still shifting objects around between three posts subject to some rules, but your goal, the objects, and the rules are a little different. First, let's talk about the goal: In the ToL, I may give you any old arrangement of the three colored balls to create from your starting position - there isn't a single outcome that you're always trying to reach. Instead, I'm interested in how you transform one arrangment into another. Second, how about those posts? The uneven height of the posts means that there is a physical constraint imposed on the moves you can make: You can't just pile up three or even two balls on any post you like! Finally, the rules are a little simpler: You still can't move an object if it has something on top of it, but you can put any object on top of another if you like.

The other interesting thing about the ToL problems we can pose subject to these rules is that the minimum number of moves is known. In the context of this study, participants were presented with problems that required a minimum of 4-7 moves, and accuracy is defined in terms of reaching the goal state in that minimum number. As you may guess, more moves also means a more difficult puzzle, so we have a nice way to parametrize how challenging the ToL is for our participants in an item-by-item way.

The final neat thing about the ToL task and the design of this study is that we can measure response time as well as accuracy. How long does it take you start moving anything at all? That is your pre-planning time, or the amount of time you spent trying to figure out a plan of attack. How long did you take between one move and the next? We can measure that move-by-move to come up with what we'll call your execution time for enacting each stage of your plan. Finally, we can do all of this separately for problems you got right and for problems you got wrong. As is so often the case in cognitive science and chess, the errors are often most important.

So, this is the key task in which these researchers found differences between the chess players and the non-players. Very broadly, this means that chess players appear to be significantly better at planning, goal monitoring, etc. than non-players, but what I find really neat about this study are some of the details regarding exactly what that looks like both when players get the answer right and when they get the answer wrong.

Slow and steady wins the race, or at least means you are VERY sure you lost.

Let's start once again with some of the easy stuff - here's what the accuracy data looks like across ToL problems of varying difficulty in our two participant groups. I'll spare you the stats and sum it up by saying that the chess players are more accurate, but the difference is especially big as problem difficulty increases.

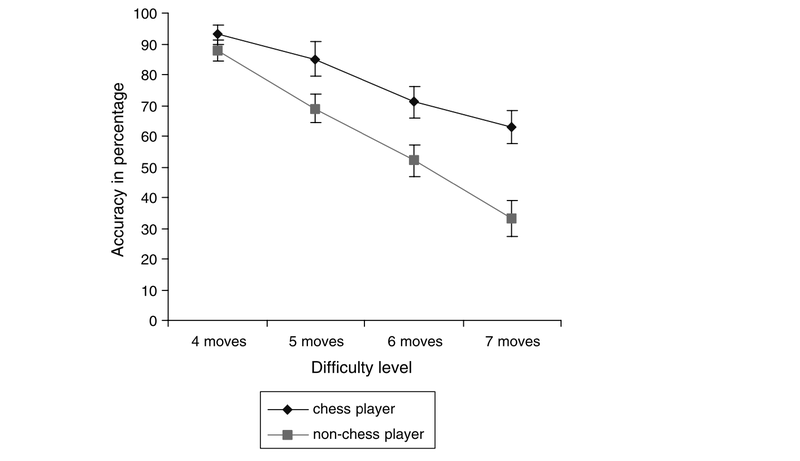
Figure 1 from Unterrainer et al. (2006) - Chess players are more accurate at ToL problems, especially for the hardest items.

Remember that we don't just have the accuracy data to look at, though - we also know how long it took each participant to arrive at a solution (right or wrong!). Take a look at the pre-planning times for both groups below and you'll see why I called this section "Slow and steady."

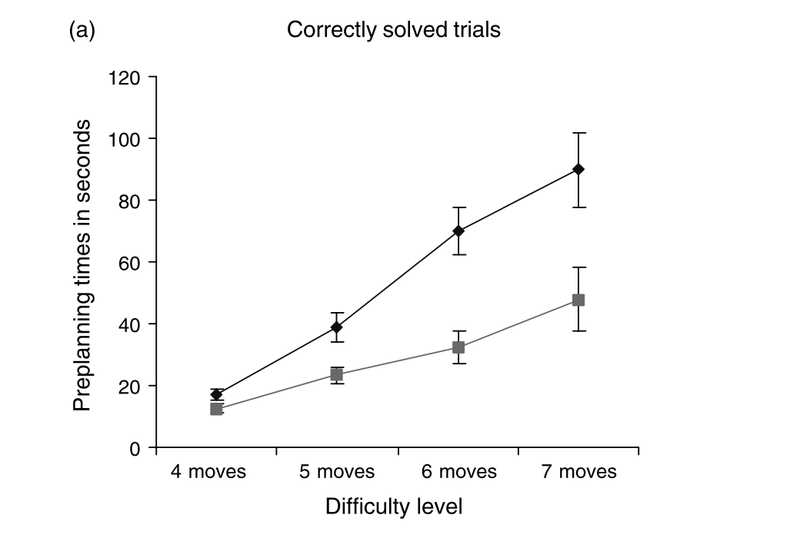
Figure 2a from Unterreiner et al. (2006). Chess players (Dark diamonds) take more time to get started on ToL problems, again with a larger difference for harder problems.

This is before you even make the first move! At the hardest level of difficulty, chess players are spending nearly a minute and a half on average - twice as long as the non-players - before even touching the first ball they intend to move. Besides the difference in accuracy, it's neat to see such a big difference in planning time. For me, it's especially weird to see a difference that's on the order of tens of seconds instead of the millisecond-scale stuff I'm used to measuring with tools like EEG or eyetracking equipment. Seconds! Who'd have thought? Besides the fact that this difference involves some big numbers for the cognitive science community, it also clearly suggests to me that this isn't at all about pattern recognition, which is assumed to be a fast process. No, this looks a lot like planning, evaluation, and decision-making rather than implicit recognition of something you've seen before. It gets even more interesting, however, when we take a look at the execution times between moves. In particular, I'm going to ignore the time between subsequent moves in a correct ToL solution to show you what happened in terms of the timing of moves when participants were incorrect. Take a look at the figure below and see if anything stands out to you.

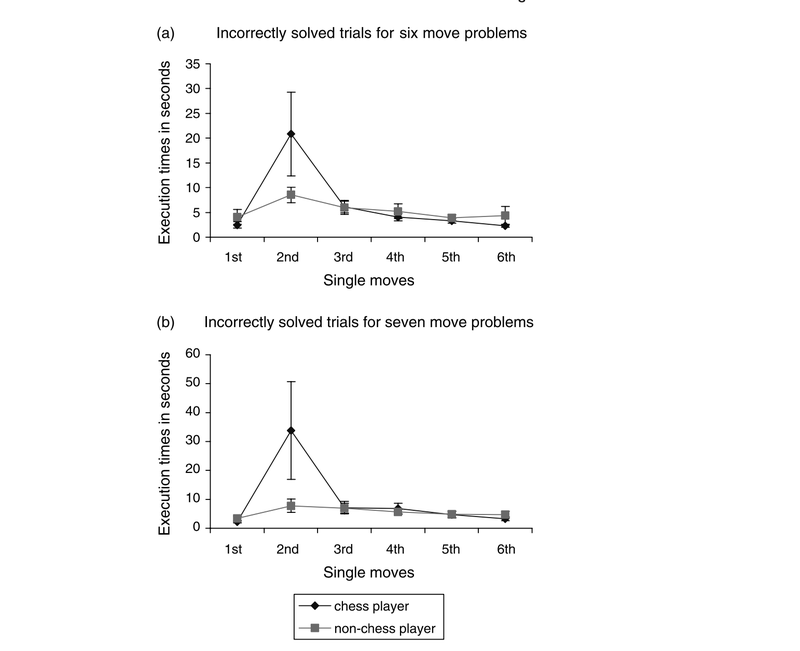
Figure 4 from Unterreinner et al. (2006). Execution times during incorrect ToL solutions differ by participant group by a lot at the second move.

I sometimes talk to my students about the "blur test" for evaluating the results in a paper they are reading. "Take your glasses off," I say, "and look at each figure with blurry vision - what still stands out to you when you can't see every little wiggle in the data?" Dear reader, this result absolutely passes the blur test. Even if you knew nothing about the study, the groups, the task, or anything at all, you would still look at these two graphs and ask "What on Earth is happening at that second data point?"

These graphs are showing you how much time participants in the two group spent on each of their moves for 6- and 7-move problems that they ultimately got wrong. What I love about this data is that I feel like it suggests something that separates these groups cognitively in terms of a specific process - error monitoring. Why is that second data point up so high in the chess player group? The authors suggest that what you're seeing is effectively an "Oh no" response: Chess players who have just made a mistake with their first move in the ToL task notice, and then they try to figure out how to regroup. By comparison the non-players just sort of sail on through, moving discs around until they find out they're out of luck. Now look, there are some important caveats here to consider. Those error bars on that 2nd data point are awfully large, which means there is a lot of variability across individuals in that data. In turn, this implies that a subset of players in the group is pushing that up rather high - are they more highly rated players? Could be, could very well be, but that isn't in the paper so I can't tell you one way or the other. The other thing to think about is whether this is actually a difference in cognitive processing or a difference in motivation: Maybe chess players are more likely to dig in and try to solve a problem they've encountered? Still, even with these grains of salt that you should take this figure with, I really like how clearly this design indicates some specific differences in cognitive performance that aren't just evident on the chessboard.

So there you have it - while I'm likely to spend a good bit of time in future posts unpacking some studies that specifically target pattern recognition and the visual processes involved in it, this was a great example of work highlighting that chess also appears to depend critically on deliberation, problem-solving, and evaluation of your own progress towards goals and sub-goals. I've also got a real soft spot for studies that keep the methods and the analyses as simple as this. Don't get me wrong, I do think eyetracking is sort of cool and my lab does do work with tools like EEG and whatnot, but deep down I'm a guy that likes trying to understand the mind with the simplest means I can come up with. I think this was a very nice demonstration of how a simple task can sometimes yield intriguing insights into how a complex task is carried out by the human mind.

Support Science of Chess posts!

Thanks for reading! If you're enjoying these Science of Chess posts and would like to send a small donation ($1-$5) my way, you can visit my Ko-fi page here: https://ko-fi.com/bjbalas - Never expected, but always appreciated!

References

Phillips, L. H., Wynn, V. E., McPherson, S., & Gilhooly, K. J. (2001). Mental planning and the Tower of London task. The Quarterly journal of experimental psychology. A, Human experimental psychology, 54(2), 579–597. https://doi.org/10.1080/713755977

Raven, J. (1960) Guide to the Standard Progressive Matrices. London: HK Lewis.

Unterrainer, J. M., Kaller, C. P., Halsband, U., & Rahm, B. (2006). Planning abilities and chess: a comparison of chess and non-chess players on the Tower of London task. British journal of psychology (London, England : 1953), 97(Pt 3), 299–311. https://doi.org/10.1348/000712605X71407

Waters, A. J., Gobet, F., & Leyden, G. (2002). Visuospatial abilities of chess players. British journal of psychology (London, England : 1953), 93(Pt 4), 557–565. https://doi.org/10.1348/000712602761381402