
freepik.com
Vampires in Chess II - The Chase
Join me in the chase of vampires. There are more of them than we could imagine!In our previous post we learned about the notion of chess vampires: legal positions without a mirror image (whose mirror image is illegal). Before continuing reading, we recommend taking a look at such post, for getting familiar with these unique creatures and learning about how to spot them if you ever come across one.
Today, we will see that the family of vampires is large and way more intricate than one would expect on a first examination. But do not be scared, remember that we are here together.
Preparing the necessary equipment
Before the pursuit starts, we need to be prepared. We cannot forget a crucifix and some garlic, but I would also like to bring with us a really special gadget. My mentor, Andrew, granted it to me when I was just a lad. Today, my friend, I would like to entrust you with my most precious tool, my vampire detector!

Characterization of chess vampires (our vampire detector)
I don't know about you, but I do not always carry a mirror with me (maybe I should). And even when I do, using it is not straightforward: I find it quite tedious to figure out what the mirror image of a position is. With our vampire detector, however, things become much easier.
Consider the dual version of chess, where Black starts the game. (I used to play this version with my grandpa, who loved the Black pieces.) Most positions can be reached both in the standard version of chess (where White starts) and in this dual one (where Black starts). But vampires cannot! Our vampire detector tells us that a position is a vampire if it can be deduced that it belongs to a game where White started.
A petit en-passant vampire
It is sensible to start with a little vampire before we go after larger specimens.
The position below was my solution to Andrew's challenge proposed in our previous post: find a vampire where en-passant is possible.
I would like to thank everybody who commented on the forum and to give credit, and a special mention, to Folichon for having solved the challenge; and to Kmenbert for getting very close. And let's not forget Whyareall, who also solved the challenge (with the exact same solution I found).

A petit vampire where en-passant is possible
This is precisely the position that Andrew also had in mind. Let us analyze why it is a vampire. The key is that it is possible to determine how many times each piece has moved (or at least whether this number is even or odd).
Analysis
The pawn on c5 has moved thrice, capturing all the way from f2. On e3 and d4, it has captured black knights, whereas on c5 it has captured the black pawn from a7, who got there in extremis, by taking the white knights on b6 and c5.
Since both white knights were captured on dark squares, together they made an odd number of moves. That, plus the 3 moves by the pawn on c5 makes an even number of moves for White. (No other white piece can possibly have moved.)
Similarly, we can realize that Black has made an even number of moves as well. What can we then conclude? That White and Black have moved the same number of times. Since it is White's turn, White must have started the game, so the position is a vampire.
Observe that the number of times that each pawn has moved is unambiguous, because they have moved in a straight diagonal. Also, note that all four knights were invested in making this possible.
Other possible en-passant vampires
We can introduce slight variations in the previous position and get other vampires where en-passant is possible. For example, we could advance the a2, h2, f7 or h7 pawns (one step), remove either queen or the f-bishops, move some of the rooks as far as we are careful with castling rights, etc. Folichon's solution is one of these potential variations.
Modulo such little changes, this was believed to be the only form that en-passant vampires could take.
Nonetheless, I refused to believe this. I was determined to uncover the secrets that the chess vampires had kept from the world since time immemorial. After many long sleepless nights, one fine day, I finally found the truth:

This metaphor expresses the fact that all other en-passant vampires (as far as we know) are based on a common motif: a race against the clock to allow one side to keep retracting.
The limited-retractions technique
After an endless search, I finally came across the following vampire. Note that there are knights on the board, but still we managed to get to the 5th rank with a pawn (and en-passant is available on b6).

An en-passant vampire with knights still on the board
At first sight, it seems ridiculous that this position is a vampire: the black queen is out and could have triangulated. However, after a closer examination, we may realize that White is very limited in retractions (backward moves).
What was the last move by White? It could not have been with the knight on g8, since this knight never passed through f6, from where it would have checked a king that never moved. (At least 4 retractions by Black are necessary before we can retract this knight, via h6.) Given that neither the white king nor the white rooks have moved, the last move by White must have been a4-a5. But how about the move before that? a3-a4? We cannot retract this pawn more than 3 times. Therefore, apart from the retraction b7-b5, we have 3 Black-retractions in order to make a white piece appear on the board, which can continue retracting for White.
But what piece could this be? The missing wQ and wBf1 never moved. The only candidate is thus the missing white knight, which was captured on d6.
However! Before we can retract the move c7xNd6, the black queen must return back home, to d8. Just like a vampire when the night is late (almost at dawn), she must go back to her coffin immediately, before the sun rises (a.k.a. White runs out of retractions).
This analysis allows us to determine with precision what the last moves of this game were. In particular, just a few moves ago we had the following position.
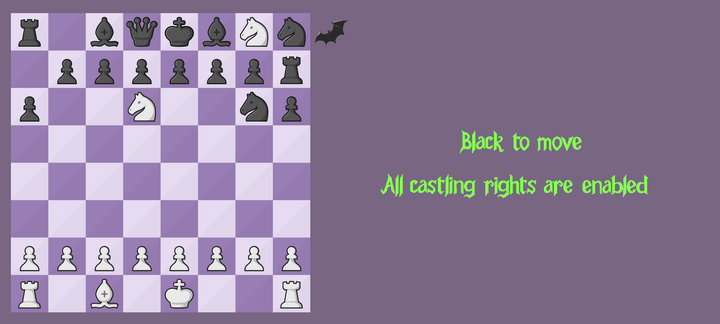
Ancestor of the previous en-passant vampire
Then, the following moves took place: cxd6, a3, Qa5, a4, Qh5, a5, b5.
Note that this last position is clearly a vampire according to our detector: it is possible to determine the parity of the number of moves made by each side and deduce that White must have started this game. Consequently, the position that we started with is also a vampire. This is because the only way to reach it is by applying the previous sequence of moves to this last position (which is a vampire).
The limited-retractions technique turns out to be a gold mine. In our final post, we will witness the full potential of this technique when facing a magnificent vampire. One that humanity had never confronted before. And thank heaven, because we were not ready. Now we are!
Challenge for the reader
The police have been hot on the trail of a new vampire who is causing chaos in the chess world. They have narrowed the search down to three suspects, but they fear all three may be infected by now. Can you help them?

Determine which of the three positions are vampires.


