
freepik.com
Vampires in Chess III - The Encounter
We culminate this series on chess vampires by analyzing a magnificent specimen.Do you have a friend who loves to challenge you with hard chess puzzles? It's your turn today! Send them this:

M. Ambrona, June 2023 (Madrid). Published at The Hopper Magazine - Issue 4.
You have just witnessed a shadow of the most complex and obscure chess vampire known to mankind. Are you all right?
A chess vampire is a legal position whose mirror image is illegal. If you haven't already, check out our previous posts to get familiar with these creatures, find out why they are important, and learn how to analyze them.
A few months earlier...
Andrew and I were excited. We had just discovered that the family of vampires was much richer than we thought. The limited retractions technique was allowing us to advance pawns without losing the parity invariant. But, how far could we get with it?
Just like we did, you may be wondering: do there exist vampires with promoted pieces?
We simply had to find out.
I tried really hard, for days. It was relatively easy to get to the 6th rank with a pawn while preserving the invariant. I even reached the 7th at some point, but unfortunately that was a dead end, that vampire could not be extended.
One fine day, I came across the above position.
I am still shocked by the fact that it exists. Let's dig into it.
Analysis
Assume that White can capture en passant. Then, the last move must have been a7-a5.
In that case, let us state a few simple facts about the position:
- White is missing the f-pawn, a knight, the original light-squared bishop and the queen.
- Black is missing the light-squared bishop and a knight.
- The missing white queen & white bishop were captured at home.
- The bishop on g8 is promoted, it is the pawn from h2 (which captured on the g file).
- The pawn on b5 came from a2 (it captured once on the b file).
- Black captured a white knight on b6.
- Black captured the white f-pawn on f6.

Assuming White could capture en passant in the proposed challenge, this position must be legal.
Now, note an important fact: White is running out of retractions!
White can perform (at most) 3 retractions with the b5 pawn and (at most) 6 with the g8 pawn (with bishop soul). This means that we have 9 black-retractions to make a white piece reappear on the board.
- Before retraction g7xPf6, the bishop on d8 must return to f8.
- Before retraction c7xNb6, the black queen must return to d8.
This last fact is because (before c7xNb6 happens) the d8 bishop has to leave to a square other than d8, c7 or b8; but this requires retracting d7-d6. The stationary pieces on a7, b7, c7, d7, e7, e8 would form a cage (a coffin, maybe?) that would prevent the queen to go back to d8 if she does not do it before c7xNb6.
Furthermore, retraction d7-d6 cannot happen until the missing black light-squared bishop reappears and goes back to c8.
Trying to retract c7xNb6 right away
It is sensible to aim for retracting c7xNb6, as it would make a white knight reappear on the board, providing White with arbitrary retracting ability.
As we discussed, such retraction must be preceded by the following steps.

Necessary steps if we aim for retracting c7xNb6 right away.
These steps require 3 + 2 + 4 = 9 retractions, plus the actual c7xNb6 makes a total of 10. This is 1 too many! White would run of retractions before we could execute all these steps.
Trying to retract g7xPf6 first
Retraction g7xPf6 will not give White arbitrary retracting power (the reappearing piece would be a pawn). However, it could "buy" us extra retractions for White. Let's give it a try.
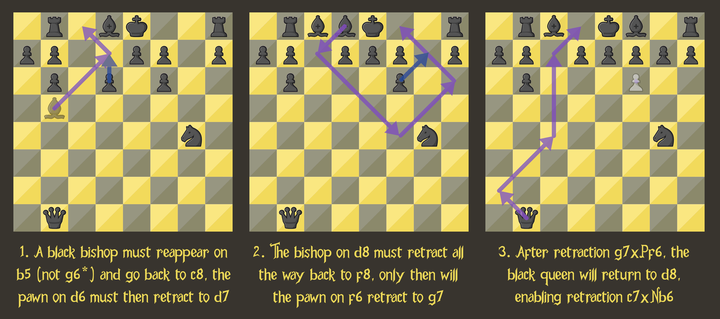
Necessary steps for retracting g7xPf6 first, and then c7xNb6.
Counting again, steps 1 and 2 require 3 + 5 = 8 retractions. It's enough, and we have one to spare!
The new pawn on f6 bought us (at most) 4 new white-retractions. If we carry the one, that gives us 5 for step 3: going back with the queen to d8 and retracting c7xNb6. But those are exactly how many we needed. We are just in time!
Final remarks
That was tight, but it seems the position from the challenge can be retracted until the initial array. However, note that:
- The black bishop must reappear on b5 (not g6). This is because it would take 3 white-retractions to make this bishop reappear on g6, but we can only afford 2 without slowing down the d8-bishop retreat.
- The capture by the white h-pawn must have taken place on g6 (not g7 or g5). Otherwise, the reappeared black knight would be an obstacle for the d8-bishop retreat.
These last details allow us to deduce that the following position has been reached at some point in this game. (Black to move.)
But this position is illegal! Both White and Black have performed an even number of moves to reach it from the starting array. Thus, it should be White to move, but it is not!
Conclusion
The position of the challenge is the mirror image of a vampire if White can capture en passant. (It is illegal.)
Thus, the solution to the puzzle is: No, White cannot capture en passant.
Vampires can be turned into nice chess puzzles like we did, because their mirror image seems legal, but it is illegal due to a subtle parity argument.
How many vampires are there?
All vampires live at the beginning of the tree of variations. And, as we have seen in previous posts, most moves lose the vampiric property (they break the parity invariant). Thus, it is not completely crazy to try to enumerate all vampires. However, this would require an automated mechanism for deciding whether or not a position is a vampire. Not an easy task, given the complexity that these beings can reach, as we have witnessed.
I hope that, one day, we finally uncover the truth about the vampire family. That we finally answer the question of whether there are more White-to-move positions than Black-to-move or vice versa. And, more importantly, whether the total number of legal positions in chess is even or odd.
I just hope that someone, out there, will continue, what we started.
I am very thankful to Andrew Buchanan, for introducing me to this topic and for very fruitful conversations. To my friend, @vonaka, who solved this post's challenge on their own, confirming that it is sound, well done! And of course, thank you, reader, for your time and interest. All the best!


