Science of Chess - Candidate Moves, David Marr, and why it's so hard to be good.

In my last blog post, I reflected on two recent Rapid losses as a way to try and identify weaknesses in my game and think about things to work on to try and improve. Some of you offered suggestions (which were very welcome!) and the nature of those comments made me think that a post about the way I think about chess improvement as a visual cognition researcher might be worthwhile. You won't find a game in this post (look for more of that soon!), but instead some of my ideas about perception, cognitive science, and trying to learn to be a better chess player.

I'll start by saying that the advice I think a lot of us see about improving our chess game is either very specific to an analysis of a particular position ("Why didn't you think about taking space in the center with 8. d5?") or broad enough that it can be difficult to apply ("Make sure you understand your plan.") These suggestions absolutely have their place, but from the perspective of a cognitive scientist, I can't help but wonder how to translate these potential areas for improvement into perceptual and cognitive processes I understand from my research. Maybe there isn't an easy bridge between these domains - to get better at chess, you probably have to spend a lot of time simply digging into the details of the game and general cognitive principles may only matter so much. Still, I think it's worthwhile at least looking at concepts from both realms to see what we might gain. At the very least, it may help us understand what there is to learn about how we learn to play chess. To get started, I want to introduce you to one of my favorite researchers from the field of vision science, where I spend most of my intellectual time away from the board.

My favorite picture of Dr. David Marr is his office. In his brief but brilliant career, he proposed an influential framework for thinking about how to study complex problems in vision science. This framework can be usefully applied to the candidate move method to identify good questions for new research into how the human mind approaches chess. Photo by Kent A. Stevens (Stevens, 2012).

David Marr's "3 Levels" Framework

The late vision scientist David Marr(1945-1980) proposed a framework for studying problems in vision science. In this framework (usually referred to as Marr’s 3 Levels) we distinguish between three different aspects of the problem: (1) What is the computational nature of the problem? (2) What are algorithms that would allow us to solve the problem? (3) What is the biological implementation of solutions to the problem?

The point of this framework was to serve as a sort of mental hygiene for vision scientists by forcing researchers to be explicit about the information available to observers and the task the visual brain was trying to accomplish with that information. Marr’s idea was that by focusing on computational definitions first, one could then be precise about the steps that might take you from a problem to a solution. Finally, one could consider whether one solution was better than another by taking a look at the brain to see what you could actually hope to achieve with real cells that sent signals to one another. For our purposes, we can focus on the mind rather than the brain and dispense with (3) straight away to focus on the first two levels. We’re also not going to use this framework to solve a problem, but instead to help us identify good questions to ask about the way we play chess.

Compared to visual problems like recognizing people’s faces or estimating depth from the retinal image, playing chess has two important advantages as a problem domain in vision science or cognitive science. First, we can formulate the problem itself precisely - to put it simply, what is the best move I can make right now? We’ll want to do better than that eventually, but for now it will do. Second, we have access to an algorithm (or model, if you prefer) that we know can solve this problem. Whether you prefer to appeal to Stockfish, Komodo, or Leela, the fact that we have chess engines that are incredibly strong means we have a procedure that gets us the right answer (or at least an answer good enough to beat GMs!). This means that if we’re thinking about Marr’s three levels very concretely, we can actually more or less complete the kind of research program he might have liked with the tools we currently have!

Let’s start with his first level: What’s the computational problem we’re trying to solve? I said that a simple way to describe this was to say that we want to know the best move we can make in a given chess position, but we can make this more specific computationally by elaborating on what we mean by a “best move.” I think a better statement of the problem is to ask: Out of all the moves that I am allowed to make, which one gives me the largest possible advantage over my opponent?

The second half of that question (the bit about "advantage") relies on something that is very relevant for the way we can think about Marr’s second level (an algorithm for solving the problem) - a state-of-the-art chess engine. A key feature of these engines is an evaluation function that assigns a positive or negative score to each position according to whether White or Black is better off and by how much. That evaluation function is part of how we might respond to Marr’s second level - What algorithm allows us to solve the problem? Here’s an algorithm we could actually use (and that Stockfish actually does use if you ask it too): (1) List all legal moves for the player who must move next. (2) Evaluate the position (assign a score) after making each move in turn and save these numbers. (3) Determine which of these numbers favors the player the most (this will either be the most negative or most positive). (4) Choose the move that matches this number, and if there is a tie, choose any of the tied options at random. Believe it or not, we can even wave in the general direction of Marr’s 3rd level (How could this algorithm be implemented in biological hardware?) by appealing to the fact that Stockfish and other engines are neural nets, meaning that there is at least a family resemblance between the way they compute these things and the way that the brain computes things. That’s a serious simplification that you should take with at least a few grains of salt, but still - we’ve done it. We’ve talked through a complete answer to this question at computational, algorithmic, and biological levels - chess is solved!

And yet.

I say this because as both a cognitive scientist and mediocre chess player, I know that the way I’ve thought about the problem of deciding what to do next runs into a lot of important constraints on how human vision and human cognition work. Here is where I think there is a lot of interesting work to be done, much of it (to my knowledge at least) largely untouched. Let’s take a look at the way we tried to approach the problem above using Marr’s framework and see how it goes when there’s an actual human mind in the loop rather than a chess engine. In particular, I’m going to say that we’d still like our human player to find the best move they can per our statement of the problem above, but I’m going to walk through our proposed algorithm to see how it would actually go. Along the way, we’re going to see how existing knowledge about vision science and cognition suggests an interesting research question about chess, the mind, and the brain.

First, what about that very first step? List all legal moves for the player who must move next. That’s easy to say (and easy to do if you’re a computer) but what about if you’re a human? In his remarkable book Thought and Choice in Chess, psychologist and chess master Adriaan de Groot takes care to quantify just how many moves we’re talking about at different stages of the game. The full graph is displayed below if you want to take a look, but the short version of the story is that we’re usually talking about at least a few dozen options.

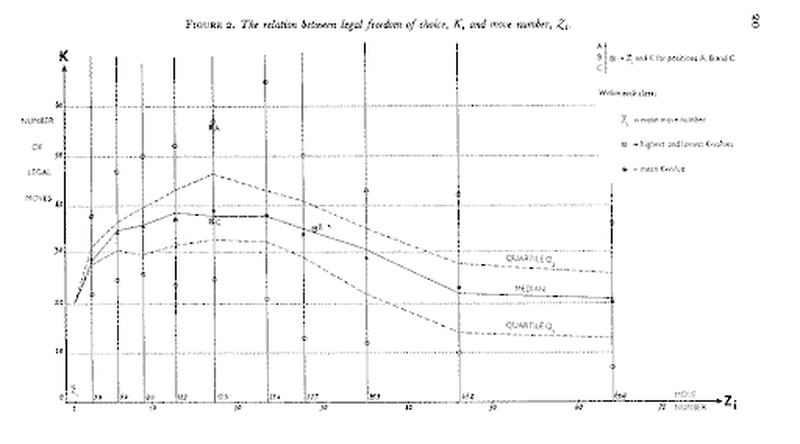
De Groot’s graph (De Groot, 1965) of the number of legal moves as a function of move number in a game of chess. We start with 20 options to consider, but this number essentially doubles (or more) by the middlegame. A chess engine can trivially work through all of these possibilities, but the human mind is far more limited and must decide on just a few moves to work through.

The trouble with that from a cognitive science perspective is several-fold. The main thing that I think about when I consider the first step in our algorithm with that number in mind are the constraints that we know about on working memory. This term refers to a component of human memory that we use to keep information in mind over short amounts of time (seconds to minutes). Depending some on how you measure it and what kinds of material you’re asking someone to remember, human working memory has a limit (or we usually say capacity) of about 4-5 items. That’s going to be a big problem for our algorithm because while Stockfish can just store moves in some kind of structure like a matrix or list, the human mind has only a few slots to use for the same purpose. If we’re wondering why we sometimes make terrible moves and miss good ones, one issue with the candidate move method for human players may simply be that we have a hard time maintaining all the possibilities available to us.

The fact that we can’t simply list and remember all of the moves we could make means that we have to use some kind of selection process to decide which moves we will consider. As soon as we’re talking about selection we’re talking about cognitive mechanisms for attention, which are closely related to both memory and perception. In general, attention refers to processes for prioritizing some things we see, hear, or otherwise sense over others - it’s useful to think about this in terms of some kind of filter that lets some things in and keeps other things out. Keeping things out is a problem for our algorithm, though, so what are the limits of visual attention in a setting like chess and how do we end up letting more of the right things in to make sure we don’t ignore brilliant possibilities? This runs right into a problem a lot of people have noted about the way writers like Kotov describe candidate moves in books like his Think Like a Grandmaster: Where do they come from? How do you arrive at the small subset of possible moves that are worth thinking through further? We know from visual attention research that it’s shockingly easy to miss things that are right in front of you - there are a number of brilliant demonstrations of a phenomenon called inattentional blindnessthat show off just how invisible something highly conspicuous can be as long as you’re allocating attention to other things in a visual scene. I won’t spoilthese demos for you if you haven’t seen them, but they are worth checking out. Even while we are paying attention to what we’re looking at, our visual system has its own limited capacity we have to contend with - your visual periphery is blurrier, for example, and subject to a phenomenon called visual crowding in which an object in the periphery is hard to recognize when it is flanked by other objects (see below). Unfortunately, chessboards are crowded spaces in both the physical and perceptual sense, potentially limiting our ability to take in a chess position all at once and interpret it correctly.

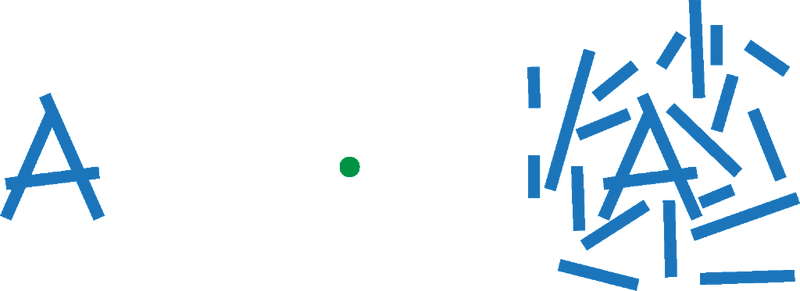
Image credit: Dr. Will Harrison. The letter “A” is easy to see at right while you’re fixating on the dot in the center, but is very hard to see amidst the clutter of lines at left. It’s the same size in both circles, but on the left we say that it is subject to visual crowding, a bottleneck in human vision that limits the fidelity of your peripheral vision. Crowding may impact candidate move selection and evaluation as you scan the board for things to do: If you’re looking at the center of the board, how easy is it to see that there’s a fianchettoed bishop, for example?

Given this fact about human cognition - both memory, attention, and perception have severe limits that mean we can ignore important information that is literally right in front of our eyes - what makes some people better at identifying candidate moves than others? One answer may have to do with how experience and study changes what moves seem salient to different players. By salience, perceptual scientists mean the extent to which some stimuli (whether they’re visual, auditory, or whatever else) stand out from others, like a bright, flashing red light while you’re driving, or a video thumbnail on YouTube that has the content creator’s face with their eyes wide open and looking right at you. High salience helps some items draw our limited attention, but this necessarily withdraws attention from other items we may need to pay attention to. If you’ve seen the first Matrix movie, you may remember the “Woman in Red” simulation in which Neo is so distracted by a salient pedestrian that he misses the deadly agent about to kill him (see below). As an introduction to both inattentional blindness and salience, it’s hard to do much better. For our analysis of the candidate move method, what makes different moves salient to a novice player as opposed to an expert? This raises interesting questions about the role of pattern recognition in chess and how it pertains to the moves that are salient to different players based on experience. Seeing a configuration of pieces again and again eventually could support a different understanding of where attention should go over a chessboard - a pointless knight trade in the center of the board may be far less interesting than the backward movement of a bishop that will allow it to shift to a different diagonal it needs access to, for example. Then again, I’ve played a lot of Scotch Gambit games as Black and I still struggle with the first 10 or so moves - what kind of training or experience helps us link board positions to better candidate moves? This runs into a number of interesting research questions in the learning sciences, including the role of strategies like spaced repetition in learning and other evidence-based techniques for improving retention of new material.

In THE MATRIX, Neo stares at a passerby that stands out from the crowd, only to be checkmated in one move by an adversary that he never even saw. I don’t know about you, but I have quite a few games that ended this way. Fair use image.

Finally, I want to close by mentioning the most important part of our proposed algorithm: The evaluation function. For our chess engines, this comes from a lot of training data that links chess positions and moves to the ultimate outcomes of games. For us mere mortals, our own evaluation function likely depends at critical point on our ability to “calculate.” But what is calculation exactly? Intuitively, it refers to the process by which we try to think through the branching possibilities that follow from a given candidate move and decide which of these is best for us. Again, though, this process has a lot of important cognitive constraints on it that will vary depending on which mechanisms we’re using to accomplish the task. Here’s a question that I think is really interesting: To what extent do different players rely on spatial reasoning vs. verbal reasoning or other kinds of cognition to calculate? What I mean by this is that my own impression of what I’m doing when I try to calculate from a position is that I sort of see the board internally and I imagine what it will look like after each move that I’m considering. For me, this is sort of a fuzzy visual image and part of my difficulty as a player is sort of “seeing” the transformed board accurately and completely after reach step. There are a lot of limits that we know about on visual imagery like this, including large variation in the fidelity of different individuals’ visual imagination. With tools like the VVIQ (Vividness of Visual Imagery Questionaire), we can at least get a first-pass look at whether different people report high-quality, vivid images in their mind’s eye or much more limited, less well-defined images. At the extreme end of this spectrum of individual differences, some people with aphantasia appear to have no subjective experience of visual imagery at all! How does this variation impact both the manner in which different players calculate and how well they do so?

How vivid are the images in your mind’s eye? This turns out to vary across individuals, at least as far as we can tell with self-report tools like the Vividness of Visual Imagery Questionnaire (VVIQ) which includes questions designed to reveal whether your internal image of objects like an apple looks more like a 1, 2 or even 5 on this spectrum. How is the vividness of visual imagery connected to the ability to calculate effectively from different candidate moves?

Imagery is not the only tool one might use to calculate, though. If you watch enough high-level chess streamers (I’m thinking of Hikaru Nakamura in particular here) you may notice that many of them rattle off lists of moves in algebraic notation incredibly quickly while they consider positions. Could this mean that some players calculate in a manner that is more about verbal or numeric information than it is about spatial transformation? I think we don’t know about this, either in terms of what players’ subjective impression is or in terms of cognitive and neural techniques for identifying the activity of visuospatial vs. verbal techniques for maintaining and manipulating complex information.

Regardless of how you try and calculate, there are other cognitive mechanisms that likely matter a ton to identifying and choosing candidate moves. Chief among these to my mind is confirmation bias, which refers to the tendency to seek out information that will support your own beliefs rather than information that might help you reject those beliefs and arrive at different conclusions. I’ve written about this before in reflecting on my own tournament play, but I hope it seems obvious that confirmation bias can be terrible for chess in general and have a specific impact on our algorithm based on candidate moves. Why? The belief a lot of us need to learn to reject is simple: This move is a great idea. By only considering possibilities that would lead to good outcomes for us after making a candidate move, we are essentially playing “hope chess” rather than critically and carefully determining what’s actually best for us. There are simple tools for overcoming cognitive biases like this, including checklists like the mantra “Checks, Captures, Attacks,” which helps us narrow down branching paths that might hold for danger for our favorite candidate move. Still, understanding how biases like these affect calculation in players of different strengths would be an exciting way to understand how the human mind adapts to the demands of a complex but constrained domain like chess and what kinds of experience or training helps it do so most effectively.

I know this is a lot, but I can't help but think about chess improvement both in terms of these cognitive and perceptual concepts and the more specific advice about studying classic games, memorizing opening lines, and drilling tactics. I hope this suggests to you that there are maybe some very interesting things to learn about how we become better at chess that deserve some good science! Stay tuned for more breakdowns of chess science as I keep trying to improve my rating and keep trying to figure out what's happening in my mind (and yours!) while playing.

Support Science of Chess posts!

Thanks for reading! If you're enjoying these Science of Chess posts and would like to send a small donation ($1-$5) my way, you can visit my Ko-fi page here: https://ko-fi.com/bjbalas - Never expected, but always appreciated!

References

Marr, D. (2010). Vision: A computational investigation into the human representation and processing of visual information. MIT press.

Stevens K. A. (2012). The vision of David Marr. Perception, 41(9), 1061–1072.

de Groot, A. (1965). Thought and Choice in Chess (2nd ed.). The Hague: Mouton Publishers.

Marks, D. F. (1973). Vividness of Visual Imagery Questionnaire (VVIQ) [Database record]. APA PsycTests.

Keogh, R., & Pearson, J. (2018). The blind mind: No sensory visual imagery in aphantasia. Cortex; a journal devoted to the study of the nervous system and behavior, 105, 53–60.

Whitney, D., & Levi, D. M. (2011). Visual crowding: a fundamental limit on conscious perception and object recognition. Trends in cognitive sciences, 15(4), 160–168.

http://www.theinvisiblegorilla.com/videos.html - A collection of compelling demonstrations of inattentional blindness.

Simons D. J. (2000). Attentional capture and inattentional blindness. Trends in cognitive sciences, 4(4), 147–155.

Nickerson, R. S. (1998). Confirmation Bias: A Ubiquitous Phenomenon in Many Guises. Review of General Psychology, 2(2), 175-220.