Why Opening Statistics Are Hard

Should we adjust for rating differences when calculating opening statistics? It is common to encounter statistics that are not adjusted or are only partially adjusted by rating. The Lichess Opening Explorer, for example, presents the raw statistics. However, the statistics are grouped by rating ranges which is effectively some adjustment. In the responses to my previous blog post, many suggested that opening statistics need to take into consideration the players’ rating difference. The idea is simple: a 2500-rated player will defeat a 1500-rated player even if he starts with 1.f3, so there’s nothing to be learned from such data points. There are many ways to do such an adjustment, some of which were discussed in the comments. For example, one can use the gained rating instead of the win rate, to deflate wins against much-lower rated opponents. Or, perhaps one can use the rating performance in the opening minus the actual rating of players. In the data section, I’m using the win rate minus the predicted win rate according to the players’ ratings.

I’ve always been skeptical about adjusting opening statistics in such manner, because intuitively it felt like the equivalent of regressing a variable (win rate) on some function of itself (rating). So, I thought I should devote some time to think about this matter a little more clearly, and concluded that adjusted estimators have their problems too, but one can argue they are actually better. Below, I present the pros and cons of using unadjusted and adjusted statistics, and I show the condition under which they are identical in theory and in practice.

1. A Standard Estimator

For the sake of simplicity, let's say that each game features one and only one crucial opening move choice for white (none for black), and then we enter the middlegame. I want to study the effect of white playing move M in some critical opening position A which arises in some games.

Assume that y is the result of the game, coded numerically (win as 1, draw as 0.5, and loss as 0). y depends on whether move M is played, indicated by the index variable I (I=1 if M is played, I=0 otherwise). It also depends on the difference in playing ability between the two players *after* M is played, which I will call m. So, I will think of m as capturing the difference in playing ability in the later stages of the game, the middlegame and the endgame. I will model y as follows, where α, and β are constants, u is a mean-zero error term, independent of the I and m variables, and i is the subscript indicating the game (note I have not included a coefficient for m, since it is not measured in any way, it’s an unobservable variable with arbitrary units):

The interpretation is that the estimator captures not just the effect of playing move M, but also the difference in m: the difference in playing ability in the later stages of the game. Assuming that those who play a better middlegame also tend on average to play better opening moves, the estimator overestimates the true effect β.

Similarly, if M is a bad move, with a negative β, and there is a tendency for worse players to play it more often, then the bias will be negative. The move will appear worse than it is. To summarize, we can simply say that this estimator is biased away from zero, making the good look better and the bad worse.

Is this bias a deal breaker? Perhaps not. If I see a move with a +5% advantage, I can still conclude that it is a good move. This apparent advantage is partly because of the true β, and partly because the move is played by better players. Since it can’t be too wrong to play the openings of better players, I might as well disregard the whole discussion about the bias and go for it. On the other hand, if there is only a +1 true advantage to be found, is the whole effort of adjusting my repertoire worth it?

Is there anyway to correct for this bias? The bias would disappear if we studied games of players with equal middlegame/endgame abilities, i.e. if we had a sample where m=0, or if at least we had some way to adjust for m. The problem is that m is unobservable: we cannot isolate the difference between two players that comes down solely to their playing abilities in the middlegame and endgame. However, we do have easily accessible data on the players' ratings, and we can construct a variable capturing the expected win rate in match i, given the two players' ratings. We can hope that such an adjustment takes care of the bias, though as I’ll show, it introduces another bias.

2. An Adjusted Estimator

Let g be the expected outcome given the players' ratings. g should be strongly related to m, but should also depend on the difference in playing ability in the opening, which I will call o. I will assume that m matters the same in games that reach position A as in all other games. I will model g as follows, with γ being a constant and ε a mean-zero error term, independent of m and o:

We see here that the adjusted estimator is also biased, if the difference in playing ability in the opening is related to the choice of playing M in position A. There are two reasons why o is not independent with respect to I. The first and direct reason is that playing move M is by itself an opening choice that raises (lowers) o, if β is positive (negative). The second and indirect reason is that people who play the good move M are more likely to also play other good moves in other opening positions in other games. Think of them as the chess players who read theory.

I’ll start by addressing the first of these two issues: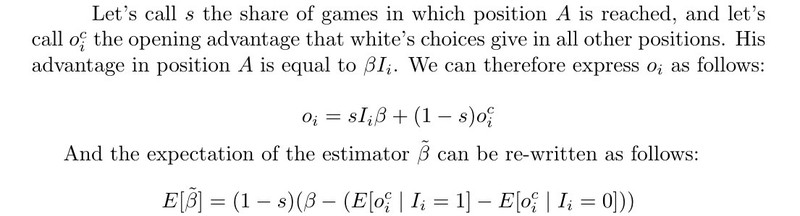

I conclude that this estimator is completely inappropriate when position A is reached too often (i.e. s is large) and M is a substantial part of a player’s repertoire. It would be biased towards zero by a lot. So, it shouldn’t be used if we want to look into first or second move statistics—perhaps no decent statistic can exist for the first moves. I wouldn’t go to the extremes though: there are so many potential problems with opening statistics, that I just wouldn’t worry about s being 10% or so.

So, let’s say that we’ll focus only on cases where s is close to zero, interpreted in a very loose manner:

The interpretation of this bias is quite tricky and less intuitive, compared to the bias of the standard estimator. Say again that M is a good move with a positive β. The adjusted estimator underestimates the true effect β, because of the term in the parenthesis. This downwards bias is due to the fact that those who play M in position A tend to also make other good moves in other positions, which increases their rating and therefore increases the rating-based expected win rate g, and decreases the term y-g.

An example: I’m a 1.d4 player and the most common replies I face are 1...d5 and 1...Nf6. Say that I know the Queen’s Gambit and Slav theory well (and score well), but I have trouble against Indian Defenses. If I study the Indian Defenses, my rating will increase and I will play against stronger players. As a result, my win rates against 1....d5 will fall! My win rate against 1...d5 depends on how good I play against 1... Nf6.

If M was a bad move with a negative β, then the term in the parenthesis would also be negative, and the bias would be positive. We can summarize by saying that this estimator exhibits a bias towards zero, as opposed to the standard estimator which has a bias away from zero.

We can also think of cases where this bias is away from zero. Say that we want to study the β of move 1.b3 (I’m taking a license here-- note I just said that this estimator is inappropriate for first moves). Assume also that we have many players who play 1. b3 as white and 1... b6 as black. 1. b3 is a decent move, so let’s assume that it has a true β equal to 0, but 1... b6 is relatively dubious. The players’ losses as black exert downward pressure on their rating, reducing g, and increasing y-g, which will then inflate the estimator.

So, what’s the correct interpretation? I think if we see a +5% advantage we should say: “those who play this move do better than they do in the rest of their repertoire by +5”. What is the rest of their repertoire though? The interpretation is much clearer if I use this estimator to analyze my own games, as it accurately points at the relative strengths and weaknesses of my specific opening choices relative to my whole repertoire.

Overall, I’m ambivalently leaning towards preferring this estimator over the standard one, but as I’ll show in a moment it doesn’t practically matter much if we have the correct sample to begin with (correct in my opinion, I mean).

3. Matching and Its Consequences

To compare the two estimators we need to take into account the fact that we only observe games that actually happen (duh). The missing/censored/truncated data problems are common in many fields (labor economics comes to mind), and researchers have found methods to correct for all that. Not too sure if such methods can be applied here, but I don’t think we care much about results of hypothetical matches anyway. I’m only interested in games that actually happen and what their statistics actually mean.

So, the issue is this: people don’t play against everybody. Higher rated players tend to play against higher rated players, etc. The matching algorithm of blitz games tends to match players with opponents in the same rating range. In tournaments, there is more mixing but still generally better players play more games against each other than against lower-rated opponents. Furthermore, and most importantly, the blitz game matching algorithm depends on the players’ ratings but not on their move choices. In other words, a player who plays M and has rating X will face the same pool of opponents as another player of the same rating X who does not play M. So, the expectation of g (which depends on the players’ ratings) does not depend on I.

This comes with some consequences, regarding the relationship between β-hat (the standard estimator) and β-tilde (the adjusted estimator):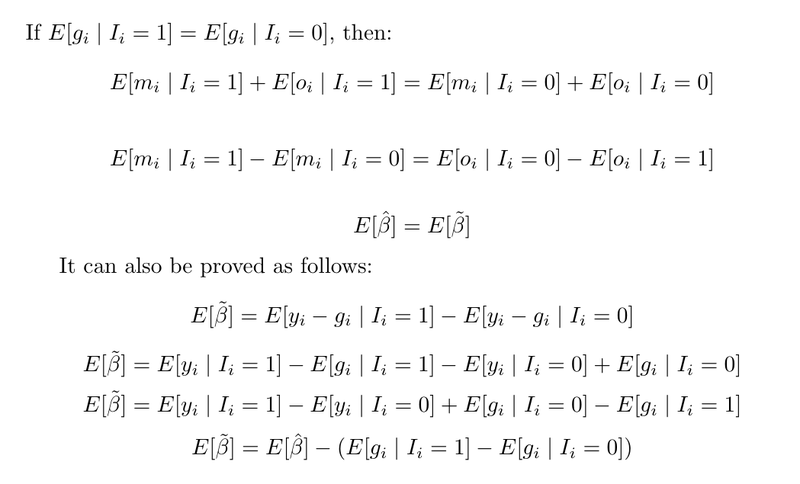

To conclude, the two estimators are identical, as long as the “if” holds.

4. The Two Estimators In Practice

I perform an analysis of Lichess Blitz data from 2016 and the first three months of 2017. I wanted easily manageable pgn files, and they tend to get a bit large after that.
The win rate is constructed as %Win + 0.5*%Draw. The adjusted win rate is constructed by subtracting from the win rate the expected result given the players’ ratings. The expected result was calculated using the standard ELO formula, which corresponds to the Glicko-2 formula when the SD's of the players’ ratings are zero. The SD's are not available anyway, so that was the only option.

The table presents the statistics for white’s fourth move in two positions which arise relatively often for many players. According to some rather rough calculations, each of the two positions is close to 5% of a player’s repertoire , and certainly below 10% (counting games as white and black, and only for players whose repertoire leads to such positions). So, we can consider the s to be small enough to not bother us.

The first part of the table includes observations based on grouping by average rating of both players in the match (the Lichess Opening Explorer methodology). The second part groups games according to white rating and the third part removes cases where the absolute rating difference is more than 150. For a discussion on the grouping methods, I refer you to my previous blog post and the related forum discussion: https://lichess.org/@/D2D4C2C4/blog/why-opening-statistics-are-wrong/VKNZ1oKw

I present the raw and adjusted win rates as their difference from the benchmark (the rates corresponding to the most common move, 4. Nf3 and 4. Qc2 respectively).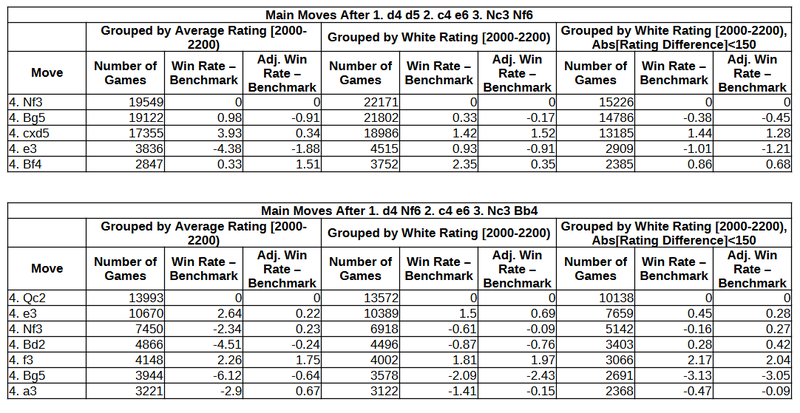

In the first part of the table, we see that the adjusted win rates are much closer to zero, compared to the raw statistics, i.e. the regular win rate. This is in accordance with the conclusion I reached earlier that the standard estimator has a bias away from zero, while the adjusted estimator has a bias towards zero. The truth should be somewhere in the middle, though I cannot think of a way to pinpoint exactly where.

In the second and third parts, we see that both the standard and adjusted estimates are virtually identical, and quite small in absolute magnitude. This is consistent with the earlier conclusion that if matching does not depend on the choice of move, then the standard estimator is equivalent to the adjusted (and biased towards zero). I suspect that the inclusion of type-A and type-D players (referenced in my previous post) who have different repertoires is what causes the first type of grouping to exhibit a divergence in the raw and adjusted win rates.

To get an idea regarding the statistical significance of the results: The differences between raw and adjusted win rates are most often statistically significant only in the first part of both tables, and insignificant in the latter two parts.

I’d like to thank @n1000, who created a subsample of Lichess Blitz Games available here: https://www.kaggle.com/datasets/naddleman/lichess-blitz-subsample. It was actually when I used the subsample data that I first realized that the two estimators give very similar results. I’m using data directly from the Lichess database here, because I needed more observations, but it’s a great resource that I’d highly recommend to anyone who wants to play around with chess data.