Let's talk about trees.

Intro

The motivation for writing this blog has been a bug in my chess program that I was too lazy to solve. Maybe that's a bit of a stretch and a bit of a lie. To be honest - I was too dumb, I did not fully understand how it was supposed to work. However, I finally managed to un-dumb myself a bit and fix the damn thing. As a result my bot should now be able to play smarter and faster. This entry will be a "Complete Beginners Guide to coding a Chess Engine". I have been telling some of my friends that I been working on a program that knows how to play chess and usually I get two responses- "I have no idea who you are. Please don't bother me or I will call the cops." or people are shocked and amazed and see it as some mystic dark magic. Well by the end of this article you will hopefully understand how to teach a computer to play chess.

As far as updates go - have fixed this annoying bug and learnt my lesson. With the gain of performance I increased the search depth by 1 and still its move times have improved. I am also close to implementing time management- that is a move is no longer searched at constant depth but is limited by time. This will hopefully allow to play some blitz and also improve the playing strength in endgames as it might afford to look deeper than before when less pieces are around. It still needs a bit of time in the oven tho. There is a minor issue where the bot doesn't go for checkmate but instead stalemates.

Evaluation function.

Evaluation function? What is this trickery? I came here for trees and I demand to speak to the manager. Well trees are just a method of searching moves. We need a evaluation function so we can give purpose and direction to the search. Otherwise we don't know what we are searching for?

The evaluation function is the heart of every chess engine. It is a simple function that digests a static position on the board and without the consideration of making any moves it gives a score on how well white and black are doing. A positive score means the computer thinks white has an advantage, negative - black and 0 or near zero it thinks it is kind of equal. Positive or negative infinity can sometimes be used to indicate that either black or white is checkmated. The numeric values it returns have usually no real meaning to chess - it's just an opinion. And only relative differences between different evaluations have a meaning- compare two moves in a position. So while most of the focus in this post and also code can often be on performing searches looking for moves, it can be that the evaluation function is the only part that actually knows how to play chess. While it is important to calculate different variations of moves if you have no clear goal what to achieve it's all for nothing.

There is so much more to this and I will certainly revisit this topic in the future

Introduction to trees.

We're going to talk a lot about trees in this article so I'll start off by an introduction to trees. In computer science a tree is a data structure that consists of interconnected nodes. There are a few very specific rules how they are connected and ordered. While not all of these rules might always apply to trees in general they certainly apply to our game tree. A node is the smallest building block of our tree. It is a very simple data structure that holds some data and can also be connected to other nodes of its kind.

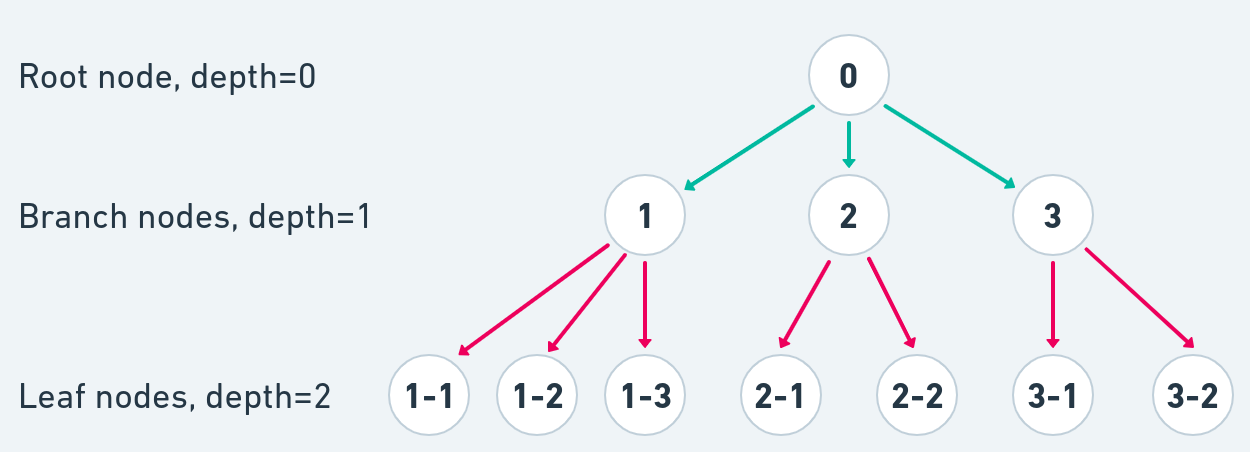
The basic concept and terminology of trees.

1. Every node has two types of connections with other nodes - a parent node and child nodes.
   1. Every node apart from the root node has one and only one parent node.
   2. A node can have none to many child nodes.
2. There are three types of nodes root node, branch node and leaf node
   1. In a tree there is one root node. It has no parent and is the only entry point to our tree.
   2. Leaf nodes have no children and are terminal nodes.
   3. Branch nodes are all the nodes in between they have both a parent and also at least one child.
3. Depth of a node is defined as the distance from the root node.
4. Breadth of a tree is the number of leafs.
5. Labeling of nodes. This is by no means universal but will help us talking about certain nodes in the tree
   1. We will label the root node - 0
   2. The children of a node will be labeled from left to right numerically - 1, 2, 3....
   3. Child nodes will have their parent's label added as a prefix so the names will end up like 1-1, 1-2 etc.

These are the basics. There is more terminology about trees and a lot of theory and classifications but these are the basics that we will need talking about trees in the context of playing chess.

Game tree search with MinMax

So what's the deal with nodes and trees? How do they relate to chess? Well it turns out trees are the best and most natural way of talking about the game of chess. A node in our game tree will represent a position on the board. This node will have child nodes that are defined by making a legal move in the position and the resulting position after the move is played will be a new node which in turn can have the it's own legal moves that result in children of their own.

It's important to note that, while we could take the root node always as the starting position of the game, we will not do that. The root node in a chess program will always be defined by the current position. We simply no longer care about past moves so for efficiency we will 'forget' everything that is no longer relevant and every move resets the root node.

So with the evaluation function in hand we now have all the components to create an algorithm that will play chess in its most basic form. The algorithm at the core of every chess engine is a MinMax algorithm which is short for Minimize-Maximize (It is sometimes called as minimax, but to me that sounds a lot like Mini Me. It is also not consistent the 'i' is added to min why not for max? Which would mean it's minimaxi, but that just sounds absurd might as well then call it minimaxipleasedoitfasti).

If you are a kid you might play what's called wishful chess- "If I go here and my opponent doesn't notice it I might take the Queen." That is trick-chess: playing for traps in hopes that the opponent will slip up. This in general is a losing strategy when the level of play is adequate. You should always try to look for your best moves and then the best moves your opponent can play in response and keep doing it deeper and deeper.

This is EXACTLY how minmax works. It just does it backwards. Let us look at an example how this works.
We start at the root node - the current position on the board. Let's say white has three available moves. Each of those moves and resulting position are represented by child nodes 1, 2 and 3. Then we look at node 1, the leftmost node at depth 1 and it's now black's turn to move and there are again 3 available moves and again we construct all the nodes. And we continue to do so until we reach depth 3 and have filled in the complete tree. Green arrows indicate white moves and red - black. The choice of depth 3 is completely arbitrary and so are the number of moves but this will suffice to illustrate the principle. Finally I calculate the evaluation for all the leaf nodes and only the leaf nodes!

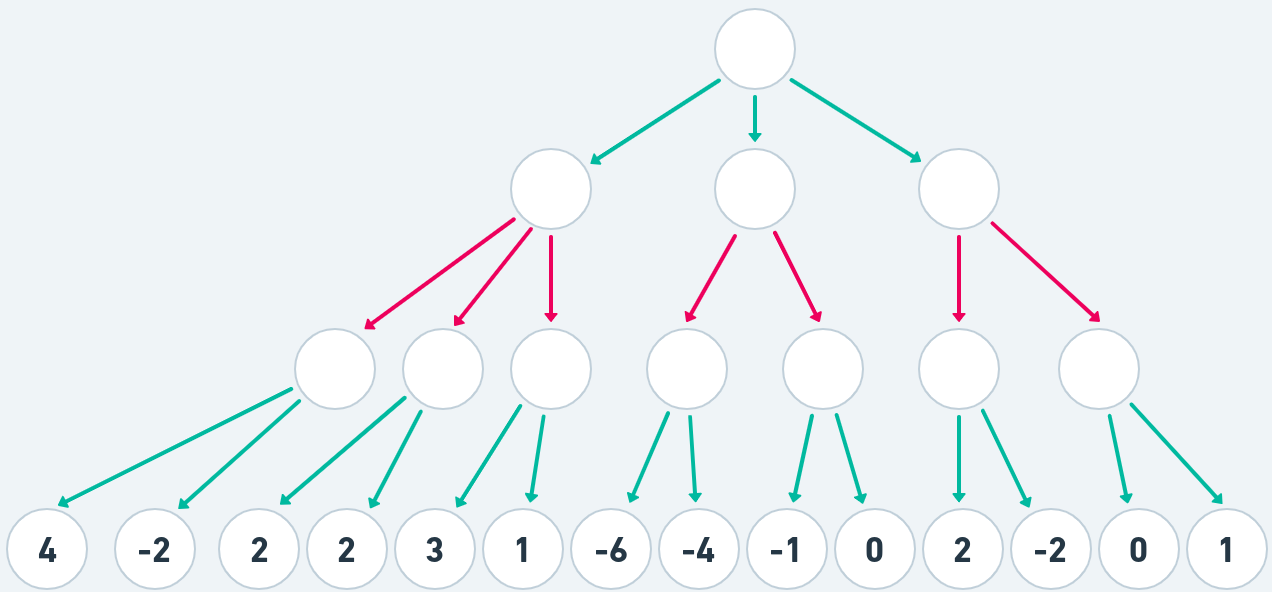
This will be our working game tree in all examples. The values on the leafs are already pre-calculated for clarity but normally they will be calculated on the fly the same time we perform our search so we don't have to traverse the tree multiple times.

The minmax algorithm will traverse down this tree to the leaf nodes and pick the best move for white (highest evaluation) and for black (lowest evaluation). We will always descend the tree starting with the nodes on the left and moving right. We start at the root node 0, We first look at the child 1. Again we look at the children of node 1 and pick the left most child - node 1-1, the children of the node 1-1 are all leaf nodes with their evaluations calculated. 1-1 represents a position where white is to move and white has two options - 1-1-1 with value 4 and 1-1-2 valued at -2. White picks the best move - 4. This value is now assigned to the node 1-1

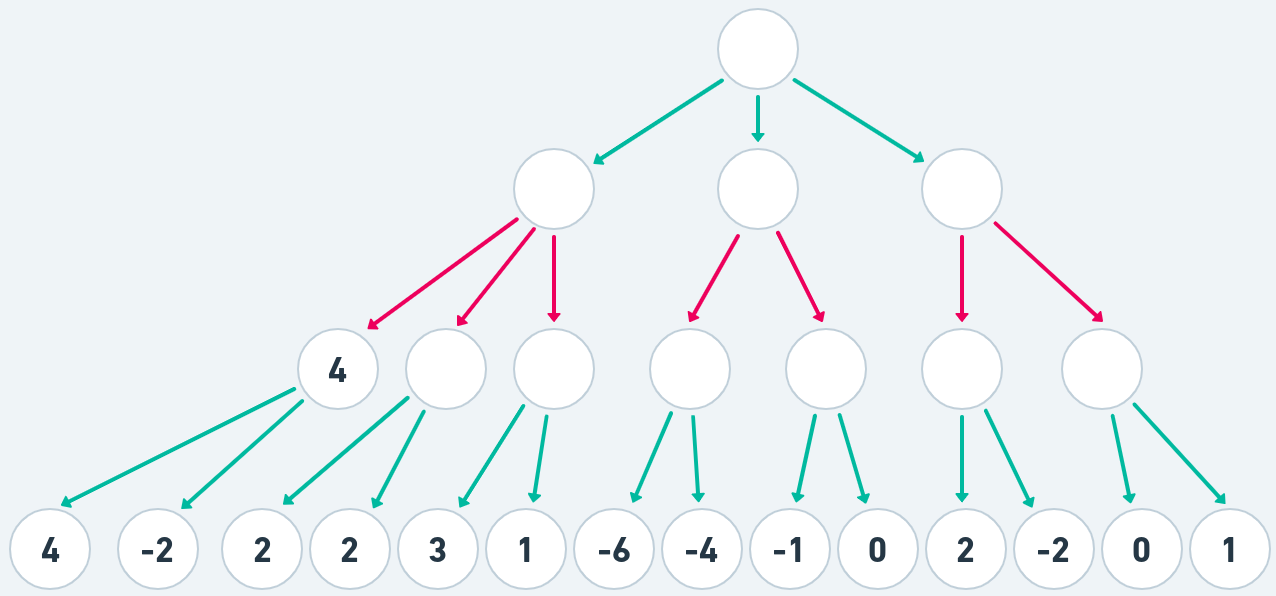
White had to choose the best move for node 1-1. Meaning picking the highest scoring of it's children.

We now repeat the same procedure for 1-2, which has children valued 2 and 2. So we just will pick the first one, no real difference. And node 1-3 has the options of 3 and 1. Picking 3. Now we have calculated all the values for the children for node 1. It is black's turn to move now. Again we pick the strongest move <em>for black</em>. This means we need to pick the node with the lowest score. The choice we have is 4, 2 and 3. We pick the lowest- 2 and assign it to the node.

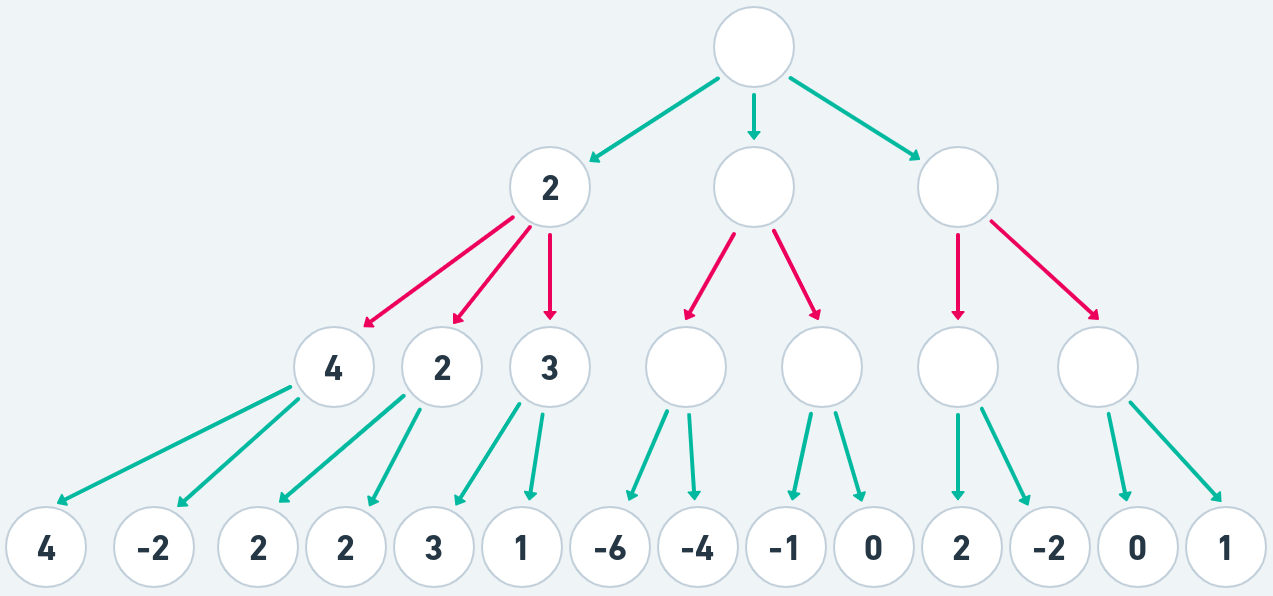
Always pick highest for white and lowest for black and fill in the tree.

It is really quite simple and you can as an exercise fill in the rest of the tree. Should not take more than a minute anyway. Black and white will pick their strongest moves and propagate back to the top of the tree and the resulting tree should look something like this: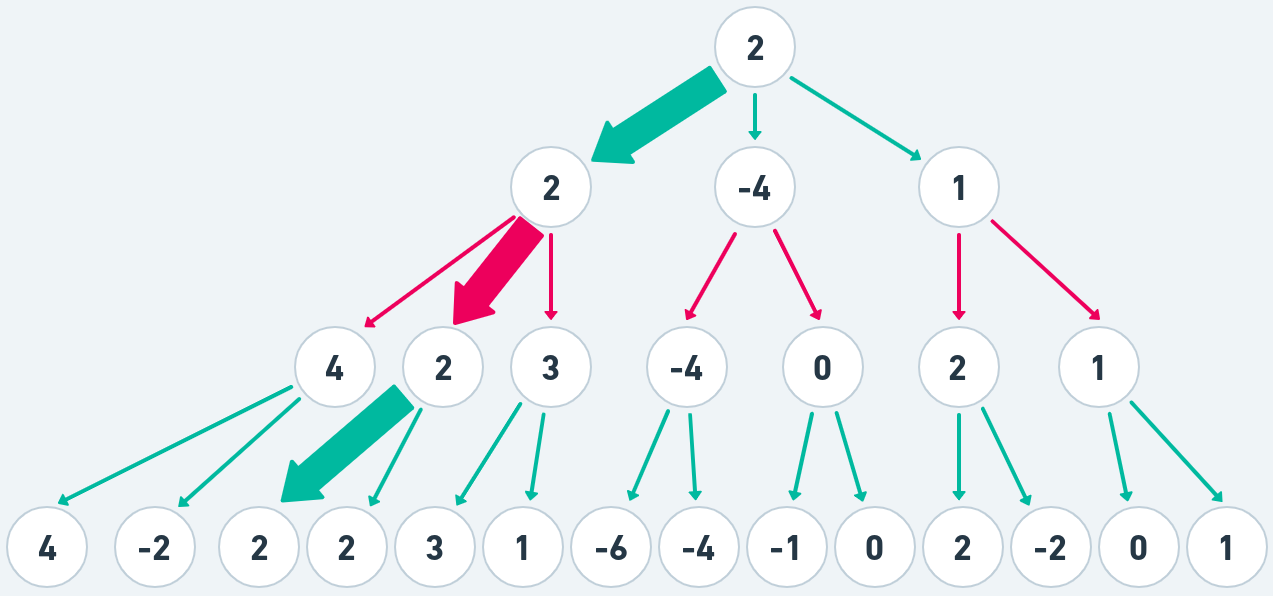

The heavy outline will be the variation both players will play out as it has the best moves for both sides

With this process we have found a path down the tree with series of moves where both black and white always played their best available moves.

This is a good introduction of how game AI works- maximize one side then minimize the other. (You of course maximize both but since black wants negative scores maximizing for black is just looking for the lowest value - minimizing). At this point we must note a couple of things:

1. Both sides played their best moves but also expected the best responses. There is no trickery involved, just rock-solid play. In contrast say white had two available moves. One where black has 20 responses. 19 out of those loses black the Queen but one actually gets white checkmated himself. The other move is just a silent move that changes nothing. A human might be tempted to play the risky move seeing how almost in all variations he gets a huge advantage and the likelihood of black finding the solution is small. This why so many people play tricky openings - gambits and traps and often with great results. These are variations that give your opponent the most chances to blunder but with best play the opponent gets an advantage. For a computer the first move is just losing since there is no assumption that black might miss the best move. So it will play the second silent move without hesitation.
2. To solve the game tree we had to traverse the whole tree - visit every node at least once and we had to evaluate all the leaf nodes. The tree I have drawn is by no means huge and it is manageable. But for real games and calculations the width and depth can be astronomical. As an example looking 4 moves deep with there being 30 moves in each position. That is 30^4 = 810k. The point I am getting at is while this certainly works and it works right it is quite dumb and very inefficient.
3. Also while in our example I had all the leaf nodes already evaluated in most cases they are evaluated only when the tree itself is searched so that one does not have to traverse the same tree twice, when it can be done once.

We can do better. We can do alpha-beta pruning.

Let's do it again but this time let us be more observant and smart. Also this time I will leave the leaf nodes blank and we only evaluate them when we reach them. Other than that the tree is identical.

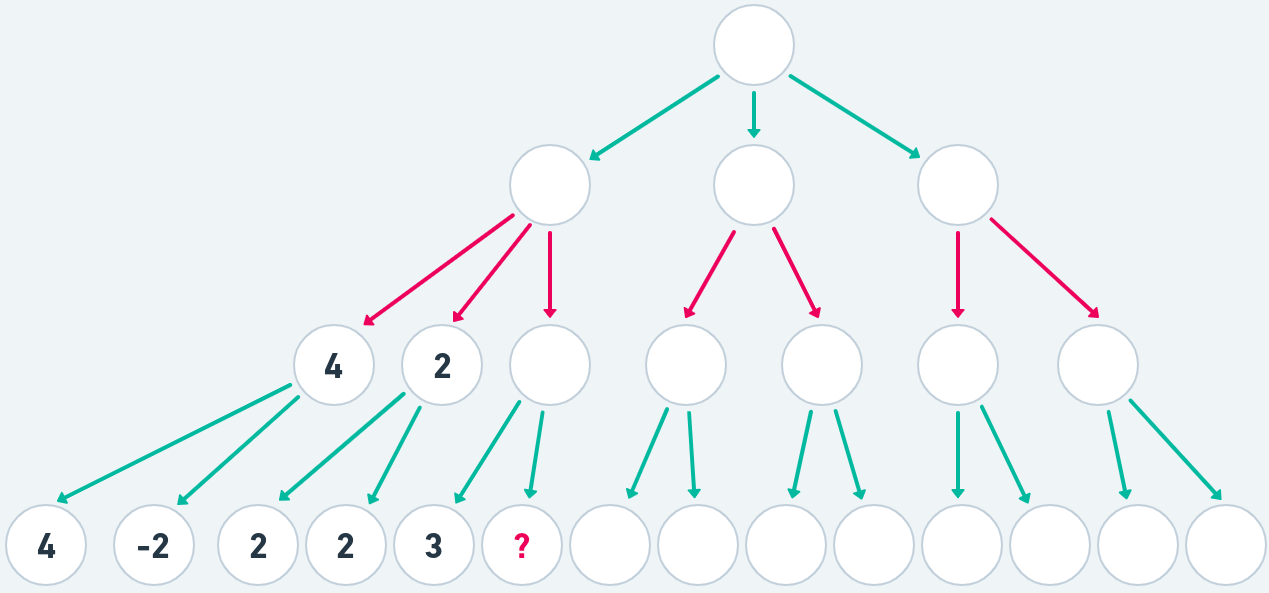
So far the tree search is exactly the same as in our minmax algorithm

We have arrived the node 1-3-2, indicated with the question mark. Minmax would now evaluate the node which we know is 1 and carry on. Let us stop and think this over... Remember each player will play their best move. We need to evaluate 1-3-2 so we can accurately evaluate it's parent 1-3. But we already know something about the parent now- the current best move (and only) is 1-3-1 which is 3. We are maximizing for white. That means if the value of node 1-3-2 is less or equal than 3 it changes nothing, because we already have a move at strength 3. The value of 1-3-2 will only affect the outcome if it is larger than 3. That actually tells us a great deal about the value of the 1-3 node it is at least 3. Let's look at the moves black is considering at node 1. It has already found moves of strength 4 and 2 and we know the last one is at least 3. That means black doesn't care what the exact value of the node is. It is an impossibility to improve the currently found 2 with a node that is no smaller than 3. So we do not care about the value of the question mark. If it is lower than 3 white will not pick it since it has a better option. If it is higher than 3 then black will not go down that branch since he has a better option 1-2: 2. So once we calculated the node 1-3-1 to be 3. We can immediately discard this branch altogether:

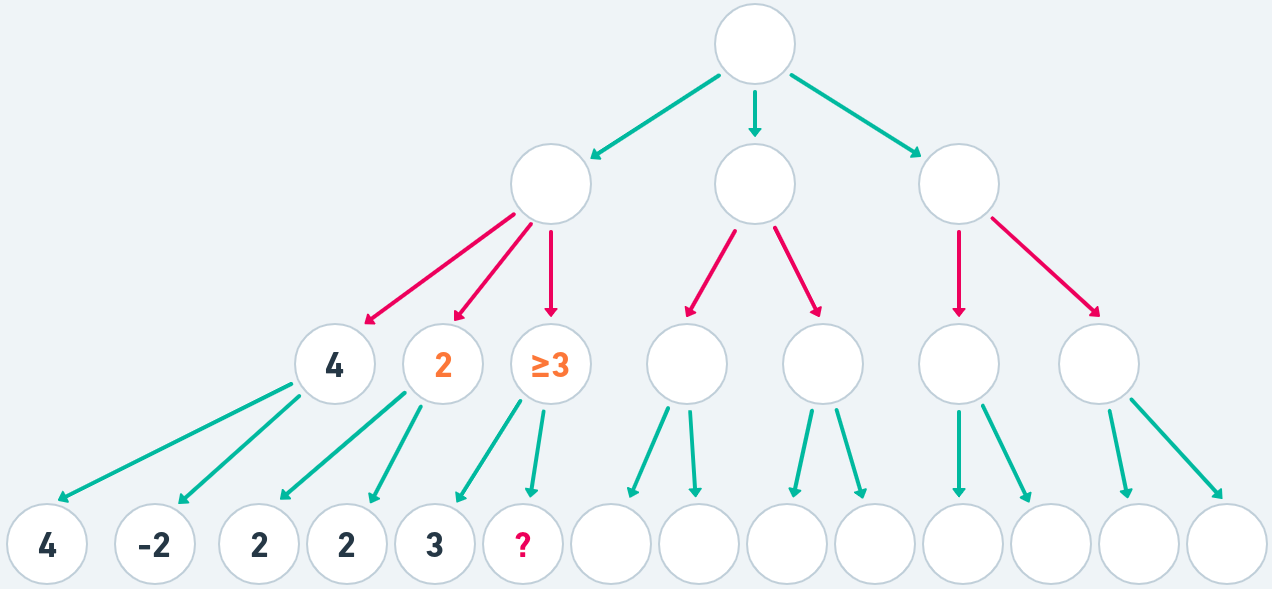
We don't know the value of 1-3-1 but we don't need to know since we already can eliminate it because it will not be reachable since both players already have better options.

The reasoning should be quite understandable but I would really encourage you complete the tree with this modified algorithm and working from left to right identify which leaf nodes and branches can be skipped as they can not be reached.

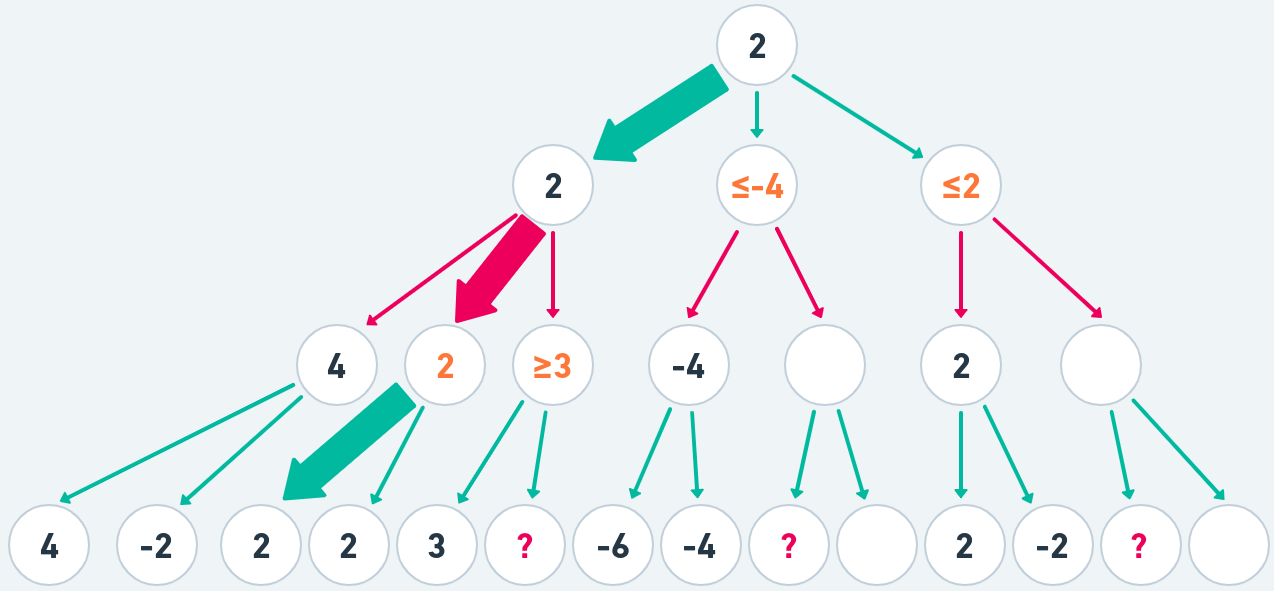
Same tree, same result but with that "work smarter not harder" attitude. The solution is simple once white calculates 2-1 to be -4, we know that node 2 will be no more than -4 and it can no longer improve on the already found node 1 of value 2. And same with the node 3. Once we find the value of 3-1 to be 2, we can stop doing any work since we can no longer improve on the already found node 1.

I hope you actually did finish the tree yourself. When I said I had a bug in my code due to laziness and stupidity it happened around here. As I had read about the algorithm. It kinda all made sense. Then I kinda put it into code and then it kinda worked. Kinda is just not good enough.

This algorithm is called alpha-beta pruning- it closely follows the best and worst case scenarios and when a branch is determined to no longer be able to affect the result it is abandoned. It will always produce the same output as the more naive minmax but it is guaranteed to work at least as fast and usually much much faster. Remember how in minmax we had to evaluate all the 14 leaf nodes. In this example we only did 9. This is actually is a very modest estimate and usually the gains are very impressive. And as a matter of fact the gains are something you can directly influence.

In alphabeta if the best moves in the tree are the leftmost nodes - moves that are looked at first, the alpha-beta cutoff points are triggered faster. When preparing this sample tree, I already made the deliberate choice to somewhat order them. Otherwise the demonstration of the algorithm could have completely failed and it might have worked exactly like minmax in the worst case scenario. But how can you order the nodes in the tree according to move strengths when you are using the tree to find the move strengths?

Well often captures can be a good choice. Or even better capturing a high value piece with a low value piece - pawn takes Queen is very likely to be a good move. Checks also often lead into forcing lines and checkmates. And the methods for guessing if a move is strong can often be very elaborate. So you can employ a lot of guess work to order moves. You don't have to always be right but if you can guess right more often right than wrong it can greatly enhance the performance. And when you're wrong - it still gives you the right result just not as fast.

In Conclusion

Well I told you how this blog will essentially give you all the building blocks of a simple chess engine.
So to build a chess engine you need these ingredients:

1. A program that can store a chess board and knows how pieces move and all the other rules. It should be able to recognize and produce all available moves in a position
2. You need an evaluation function. There is no point in knowing how the pieces move if you have no sense of quality. We must be able to differentiate between terrible positions and good ones.
3. Search algorithm. Once we know how pieces move and have a sense what positions are good and which are bad we can generate our game tree and start searching for moves that will result in the best position.

That is really it. The first point of course is trivial if you have basic programming knowledge. The second and third points are where the real strength of engine play comes from. A lot of of early computer chess had a weakness in positional play- they didn't much care about chess principles like activity, space, king safety and pawn structure. So when people would play those old machines - the best strategy was to do nothing and wait for the machine to make strategically unsound moves and damage it's long term structure. The machines would happily do that- because they had an extra pawn or bishop for knight. Some of the greatest leaps in computer play were achieved through better evaluation. Kasparov himself accused DeepBlue of playing too much like a human to the point where it was implied that there could be some foul play at hand.

Efficient search is king. If machines would just employ the naive minmax algorithm then I doubt their level of play could reach that of a good amateur. The move ordering and guess work involved is pretty impressive, the engines also selectively choose to analyze some lines deeper than others and have actually becoming more human like in their internal working than the old dumb machines that just crunched numbers real fast. My next blog post will hopefully look into this dark magic of guessing and should be more about chess than maths and code.