Identifying Brilliant Moves With Leela Chess Zero
One of the most captivating things about chess are brilliant moves, moves that are unexpected, beautiful and in addition very strong. But seeing the beauty behind such moves can sometimes be difficult as an amateur, so I looked if chess engines can help me identify brilliant moves.Firstly, one needs to define what makes a move brilliant. This is not easy, but I think that two important properties of brilliant moves are:
- They are surprising
- They are the best (maybe the only good) move
Checking the second point is easy with engines. However, it is very difficult to determine when a move is surprising to a human. That's where LC0 comes into play.
Technical Background
LC0 has a policy and a value output. The value is basically the evaluation you see of the position. The policy is a list of probabilities for each move with which an automatic player would make that move. In other words, it gives Leela's 'intuitive' likelihood of a move. I use this percentage to determine how surprising a move is.
So when looking for brilliant moves, I first use LC0 to determine how surprising a move is and if it's probability is lower than a certain threshold, Stockfish will check whether the move played in the game is also the best move.
Some examples
The first thing I did in order to verify that the program can identify brilliant moves was looking at various famous brilliant moves in order to see what LC0 and Stockfish have to say about it. Note that I used a probability threshold of 2.5% for the following positions.
The first move I think about when somebody mentions brilliant moves was played in Topalov-Shoriv, 1998 in the following position:
Here Shirov played 47...Bh3!! which is one of the best moves of all time.
This is detected as a brilliancy and LC0's policy gives it a probability of 1.34% and it's by far the best (maybe the only winning) move according to Stockfish.
Fischer-Benko, 1963 is another famous example:
Here Fischer played 19.Rf6!! which stops black from playing ...f5 (for example: 19.e5? f5! blocking the b1-h7 diagonal).
LC0 gives this move a probability of 1.4% and it is the only winning move according to Stockfish.
One example, that isn't surprising at all to LC0 is Short's amazing king walk in Short-Timman, 1991:
The game continued 31.Kh2! Rc8 32.Kg3 Rce8 33.Kf4 Bc8 34.Kg5 1-0 The most surprising move for LC0 was 32.Kg3 but even that move has a probability of 7.49%. This shows just how strong LC0 is without even calculating any lines and playing just on 'intuition'.
Too many brilliancies?
The natural follow up question now is if the program detects to many brilliancies. To test this, I looked at all games from the 1959 candidates tournament.
In 112 games, the program found 9 brilliancies. Looking through them, there are some very nice moves, but also some confusing choices.
One good example is from Petrosian-Olafsson, 1959:
Here Petrosian played 25.Ra2!! LC0 only has a probability of 0.92% for this move and it's the best move according to Stockfish. However, there are many other good options for white. I think that this move has a nice point to it, but it wouldn't usually be called a brilliant move.
One very beautiful tactical move in Tal-Benko, 1959 was also marked as brilliant:
Tal played 23.Bf8!! which clears the h6-square for the queen. This move has a probability of only 0.8% according to LC0.
You can find all the brilliant move in my study where I commented with the probabilities for the moves.
Final Remarks
Looking over the games of the 1959 candidates tournament showed that some "brilliancies" found this way wouldn't qualify as such when a human would judge the moves.
Another thing that might be changed is that brilliant moves are clearly better (whatever that exactly means) than all other moves since I imagine that the probability of a strong move is much lower, when there are many good moves to choose from.
However, I still think that this project was very interesting as it gave me some insight into how LC0 works and pointed many beautiful moves out which I wouldn't have seen otherwise.
If you enjoyed this post, please check out earlier posts of mine, where I use LC0 to evaluate sharpness and where I use this sharpness value to compare different openings.
More blog posts by jk_182
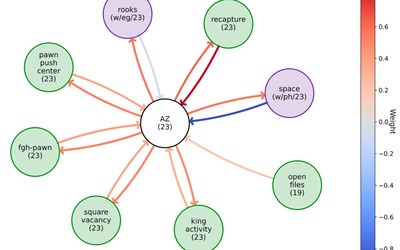
Concepts Discovered by AlphaZero
Looking at a paper from DeepMind about concept discovery and transfer
Using Stockfish to automatically find Tactics Puzzles
Can an engine find a tactical puzzle by itself?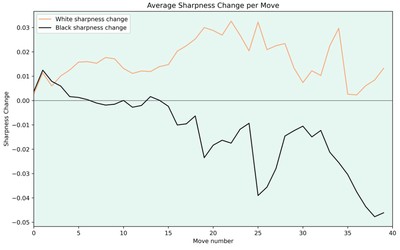
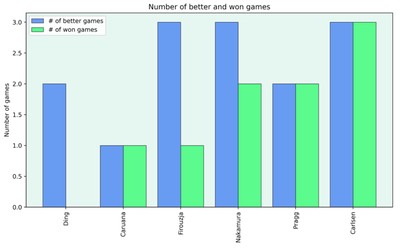
Analysing Armageddon Games: Time Usage, Scores and Sharpness
Taking a closer look at armageddon games from Norway Chess