lichess.org
Donate

Lichess Accuracy metric

The Accuracy metric indicates how well you play - according to Stockfish, the strongest chess engine.

An accuracy of 0% means you only played terrible moves; 100% means you played all the preferred Stockfish moves.

What accuracy percentage is considered "good"?

It is flawed to compare accuracy to a numerical grade you would get on a test. In more complex positions it is harder to find the best moves, so your accuracy might drop accordingly. Conversely, in lopsided positions most moves don't change the winning chances meaningfully, so the accuracy score may be high even if your conversion of the position wasn't clinical. While Stockfish can assess the soundness of our moves, it can't tell us how difficult it is to find them.

My opponent had an accuracy of 96%. Were they cheating?

A very high accuracy percentage isn't necessarily indicative of superhuman, "GM-level" play. If you blunder early on or play consistently subpar moves, your opponent will have greater chances to capitalize on your mistakes. This can lead to a very high accuracy. That said, if you suspect your opponent was cheating, please use the report form.

Do higher-rated players have a higher accuracy score?

While there is some correlation between the players' ratings and their accuracy, it is not straightforward. A more skilled player tends to play more principled, theory-heavy openings and put more tactical pressure on the opponent. This can create more complicated positions and provoke inaccurate play on both sides. Moreover, lower-rated players are often more reluctant to resign. As we discussed above, protracted lopsided endgames can increase the accuracy score.

How exactly is it computed?

Accuracy% represents how much you deviated from the best moves, i.e. how much your winning chances decreased with each move you made. Indeed in chess, from a chess engine standpoint, good moves don't exist! You can't increase your winning chances by playing a move, only reduce them if you make a mistake. Because if you have a good move to play, then it means the position was already good for you before you played it.

First, compute Win%

Win% represents your chances of winning the game from a given position. It's based on a Stockfish evaluation in centipawns. We then apply an equation to make it more intelligible:

Win% = 50 + 50 * (2 / (1 + exp(-0.00368208 * centipawns)) - 1)

It looks like this:

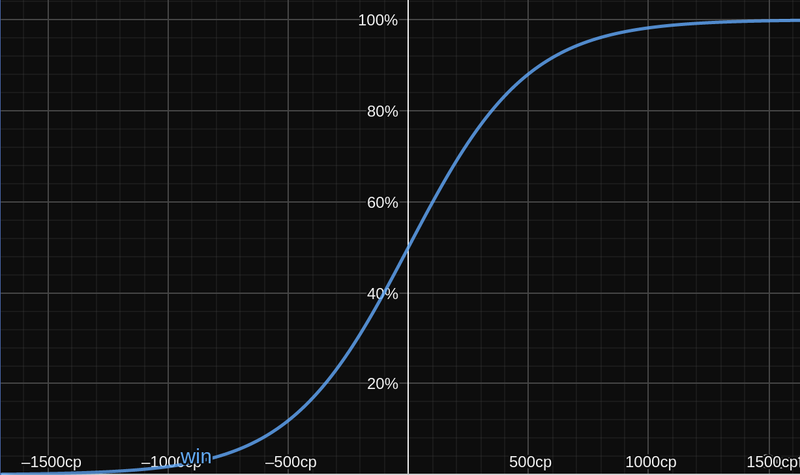
Win% by Stockfish centipawn evaluation

Here's a link to the graphed equation, and another the Lichess source code implementing it.

The equation is based on real game data. Note that we might update it in the future, to better map centipawns to win chances.

Then, compute Accuracy%

Now that we have a Win% number for each position, we can compute the accuracy of a move by comparing the Win% before and after the move. Here's the equation:

Accuracy% = 103.1668 * exp(-0.04354 * (winPercentBefore - winPercentAfter)) - 3.1669

It looks like this:

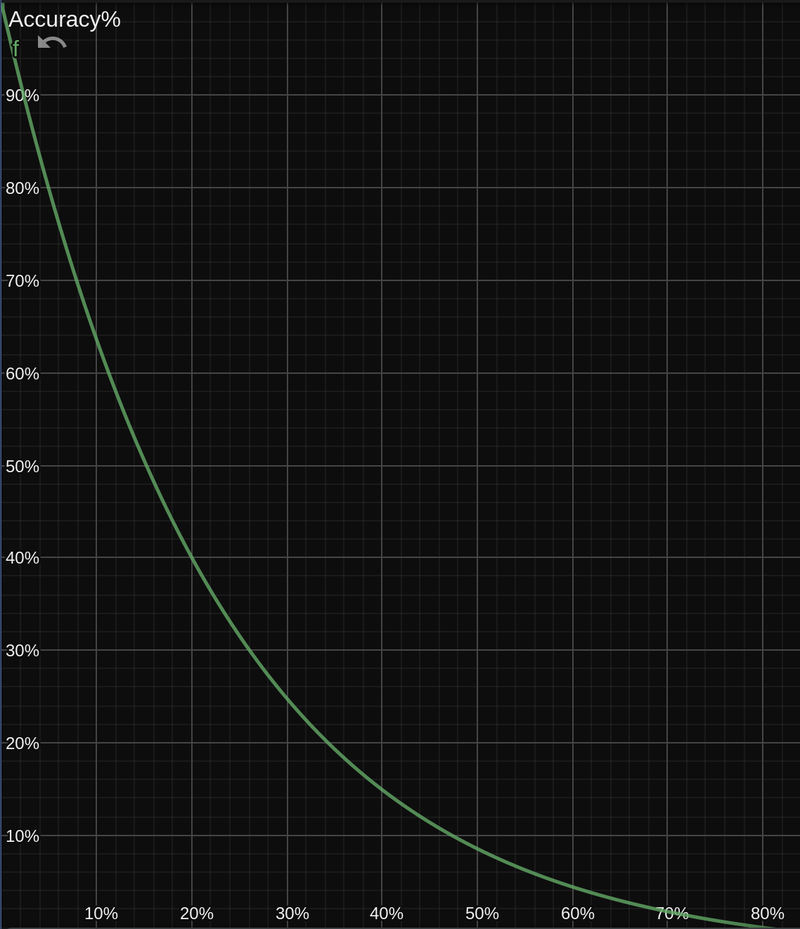
Accuracy% by difference of Win% from a position to the next one

Here's a link to the graphed equation, and another the Lichess source code implementing it.

Note that we might change this equation in the future, to better map Win% to move accuracy (Accuracy%).

Why not just use Stockfish centipawns?

Centipawns are great for developing chess engines, which is their main use. But not so much for human comprehension.

A major issue with centipawns is that they're dependent of the position evaluation. For example, losing 300 centipawns in an equal position is a major blunder. But losing 300 centipawns when the game is already won or lost makes almost no difference and is largely irrelevant.

Thus, "300 centipawns" has no meaning on its own for a human. That's the problem we aim to solve with Win% and Accuracy% . These new values are derived from centipawns, but they try to be independent of the position evaluation. 30 Accuracy% should mean the same thing whether the position is equal or winning/losing.

Also see Centipawns Suck by Nate Solon.

Where are Win% and Accuracy% used?

Lichess has been using these for years, to identify inaccuracies/mistakes/blunders in game analysis.

They're also visible and usable in Lichess Insights. Examples:

They may become visible in other parts of the site in the future.

I analyzed my game on both Lichess and Chess.com and got different accuracy scores. How is that possible?

There is no universally accepted way to compute accuracy percentages. Different websites use different formulas, engines and analysis depths. On Lichess, the server-side analysis is carried out by the latest Stockfish NNUE. We use games among 2300-rated players as a benchmark to determine empirical winning chances.