When should you berserk?

Your goal in a Lichess arena tournament is to accumulate the most points possible. A win gives 2 points, a draw 1, and a loss 0. If you are on a win streak of 2 or more games, then you earn double points (so that a win gives 4 points and a draw 2) until you fail to win a game. Additionally, at the start of any game, you can choose to berserk: you cut the time on your clock in half, but if you win you get an extra point. Of course, having less time should generally make winning more difficult. So the question arises: what policy should you follow to maximize your points in an arena tournament given this unique payoff structure? For example, you might think to play more conservatively and rarely berserk, focusing on prolonging win streaks to get double points as often as possible. Or you might attempt to play as aggressively as possible and berserk often, reasoning that the extra points you get from berserk game wins will outweigh the double points you'll lose out on when you do end up losing win streaks. I've attempted to provide a somewhat rigorous answer to this here, using modeling informed by data from actual Lichess arena tournament games.

I became interested in this question from watching Lichess Titled Arenas and Blitz Titled Arenas, so for now I've only looked at 1+0 and 3+0 arena tournaments (these are also the standard time controls for regular Bullet and SuperBlitz arenas). If you would just like to see the final results, skip to the images at the end of this blog. Otherwise, if you would like to read a bit about the modeling process, read on. (For even more information, and all code used for this project, see the repo on GitHub.)

It turns out that playing in an arena tournament can essentially be viewed as a Markov decision process (MDP). The figure below demonstrates a simplified model. At the start of every game, you are always in one of three states corresponding to your current win streak: the nodes 0, 1, or 2+. There are two possible actions in each state: to berserk (red lines/nodes) or not (blue lines/nodes). And for each state-action pair, there are two possible results: win or lose (in this simplified example we're not including draws). Each of these possible results has a reward associated with it: the points you earn (green numbers). Finally, for each state there is some probability (possibly 0) that the current state-action pair will transition you to that state (only the state-action-state transitions with non-zero probability are depicted in the figure).

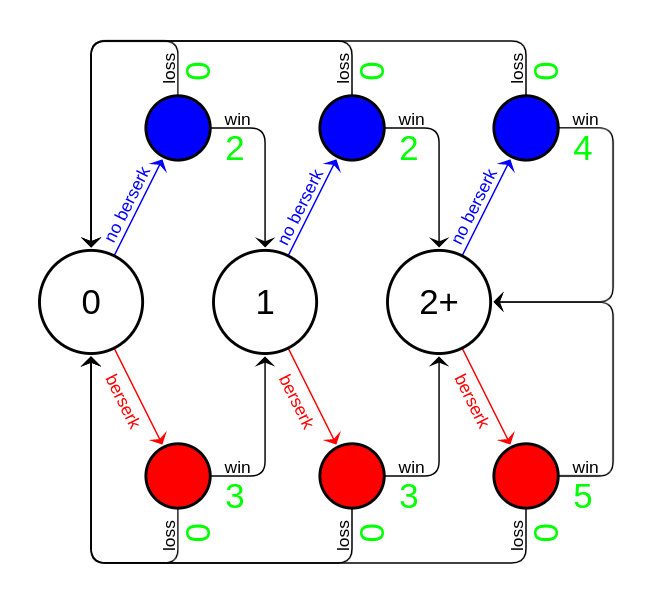
Once you have formulated a given problem as an MDP, there are standard techniques to determine the optimal policy that maximizes the total reward over time. In our case, we just need to go beyond the simplified example by adding some more dimensionality to the state space. Specifically, we consider that each possible combination of these factors is a state: your current win streak; your color in the current game; your opponent's rating; whether your opponent berserked. Also, of course, we include the possibility of draw results. With this MDP formulation in hand, all we need to calculate the optimal policy is a model that estimates all the state-action-state transition probabilities.

To find such a model, I looked at all 1+0 and 3+0 arena tournament games in the Lichess database from April 2017 to December 2021. This amounted to ~71 and ~99 million games, respectively. I then fit three models to the data:

• A logistic regression model to estimate the win-draw-loss probabilities for any given game, given white's rating, black's rating, and whether each side berserked.
• A logistic regression model to estimate the probability that either white or black berserks in any given game, given white and black's ratings.
• A model to estimate the probability of being matched with an opponent of a certain rating, given your rating.

Combining these three models allows us to calculate the state-action-state transition probabilities for the MDP. And with the MDP fully specified, we can calculate the optimal policy.

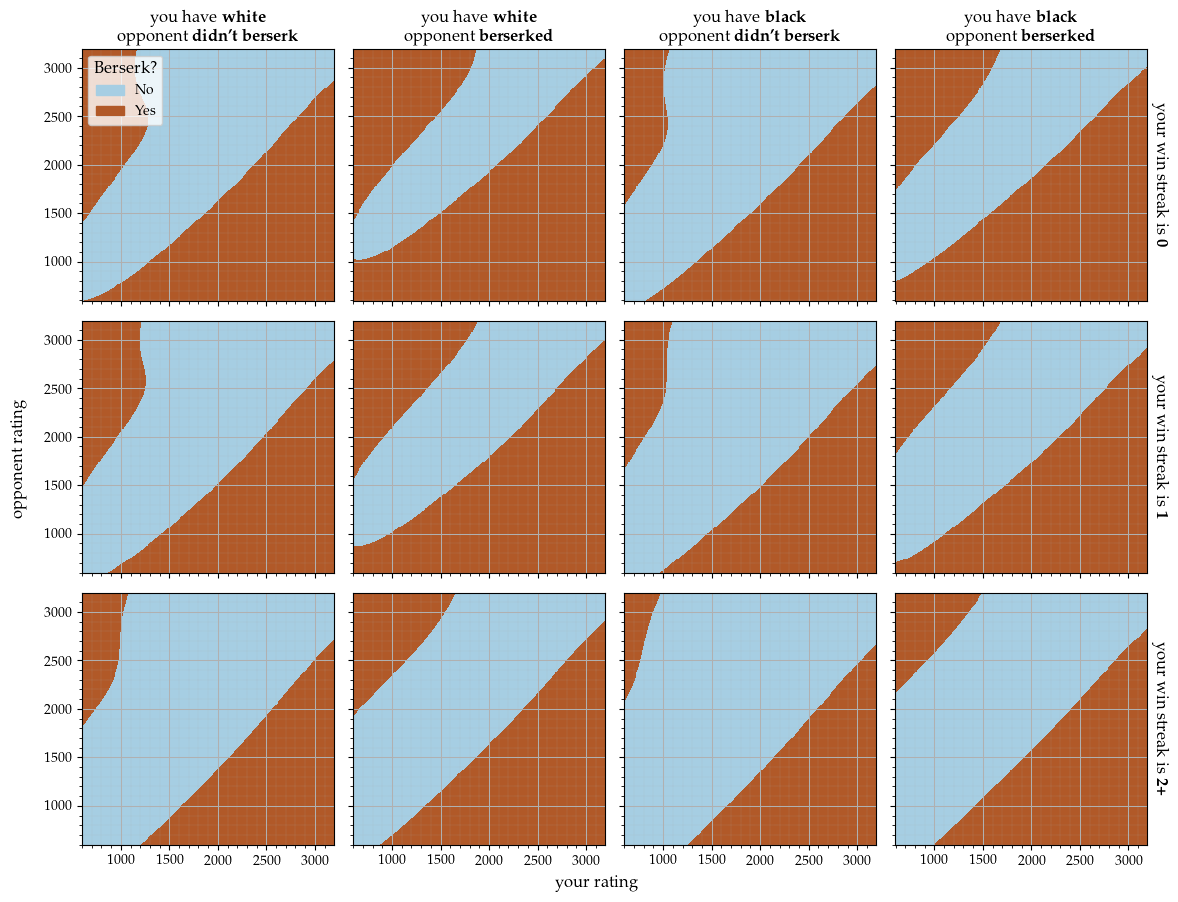
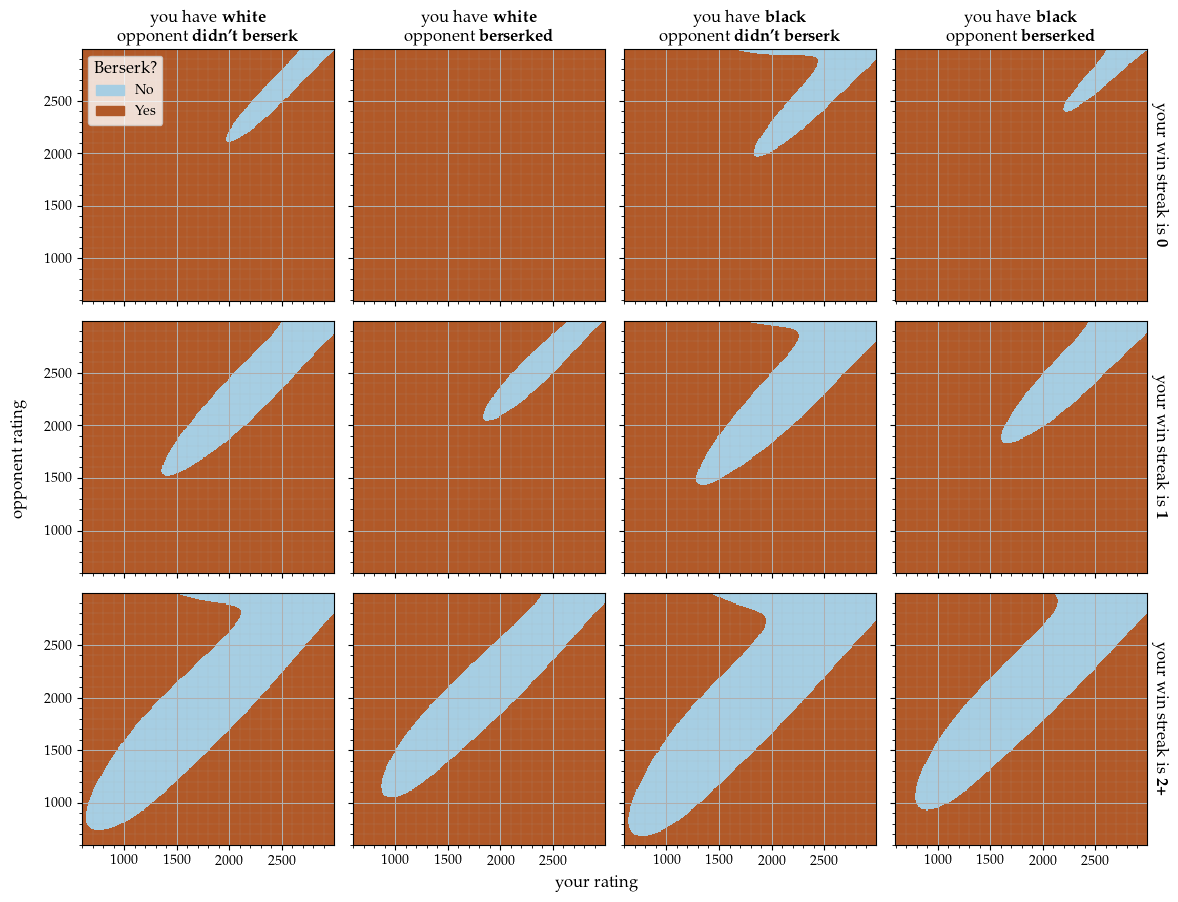
In both of the following figures, each plot in the grid corresponds to one of twelve scenarios, determined by the combination of: your current win streak, the color you have in the current game, and whether your opponent berserked. The relevant plot for each scenario is at the intersection of the corresponding row and column.

Berserk policy for 1+0 arena tournament games

Berserk policy for 3+0 arena tournament games

Conclusion

This was just one way of modeling this question, and all models are wrong. I made certain assumptions and simplifications, so that the above images might not give exactly the optimal policy for you in every moment of the exact arena tournament you're playing in. (You can find out more about these if you sift through the materials in the repo I linked above). But hopefully this has at least provided you with some interesting food for thought on this question.