You can't have more than 218 legal moves to choose from.

Ever since Nenad Petrović, grandmaster of chess composition, published his 218 move composition in 1964, people have tried to come up with a better one. Last month, I joined the hunt and, being a computer scientist, I decided to settle this question once and for all, using computers. You can give it a try yourself. Try to find a position with more moves than the one below.

Spoiler: You won't.

Reachable chess position with 218 moves for White, published by Petrović in 1964.

...but how can we know for sure?

By checking all approximately 8.7x10^45 reachable chess positions?
Yeah that's not gonna happen...

That's 8.7 billion billion billion billion billion and it's enough to scare even the mightiest of supercomputers. In fact, cracking AES-128 encryption would be easier.

Fortunately, we can use the power of Math!

Follow me along and perhaps you can compute yourself a world record afterwards :)

Using the power of Math

Red is the official color of Math, at least in my elementary school.

We're gonna tackle this problem from the white side, i.e., it is White to move. Except for rare exceptions regarding the reachability of positions, this is equivalent.

Since proving that a position is reachable is complicated, we're gonna search through all ways of placing pieces on the board and filter out the non-reachable ones later on, if needed.

Obviously, 99.9% of the positions suck at having lots of moves, they are not even close to 218. We just need a way to skip them and pray that there exists enough electricity to check the rest.

Let's begin with a couple of useful observations.

Useless pieces

A black piece does not improve the number of moves, most of the time. Its existence only benefits the number of moves if it increases White's number of moves, i.e., at least one of the following is true:

• It can be taken by a white pawn, giving said pawn more moves
• It protects the black king from check, making an otherwise illegal position with lots of moves legal
• It frees a white piece from being pinned to the white king, thus giving it more moves

Otherwise, it is useless, at best, and thus can be removed.

I inserted this picture for the sole purpose of making this article look less text-heavy.

Too powerful pieces

Next, we observe that, if piece counts permit, we can always replace a black piece, with the exception of the black king, with a strictly less powerful one. That is, a piece that has a subset of the moves of the original piece. For example, a queen with a pawn/bishop/rook or a bishop with a pawn. Except if a pawn is on the seventh rank, since in that case, each of its moves to the promotion square counts as 4 separata moves. The only way for Black's moves to affect White's number of moves is by pinning White's pieces or preventing the white king from stepping on a certain square. Both of these things can't get worse if the black piece has less moves than before.

Too weak pieces?

The other way around, it is not so easy, however. You'd think that you can just replace white rooks and white bishops with white queens if counts permit, but the problem is this: How do you ensure that you cannot capture the black king, making the position illegal? Maybe the optimal solution has a rook instead of a queen to avoid just that?

Well, you might say "Let's just place a black piece in between then".

And you would be wrong unless you can tell me why you haven't just blocked some other white piece and thus reduced the number of moves in total. Or what your plan is, if there is no space to put something in between. You just made the position illegal, duh!

No checks, thank you

Finally, we can get rid of checks. If the black king is in check, it means that the position is illegal, since it is White's turn to move and they could just capture the black king. Not okay! So that can't be it. On the other hand, if the white king is in check, then the number of White's moves is severely restricted and we can easily prove that we cannot reach 218 moves. There are three ways to get out of check:

• Move the king
• Capture the attacker
• Block the attack

Moving the king gives 8 moves at best. Since any square can be reached by at most 16 pieces at the same time (8 knights and 8 other pieces straight or diagonally), capturing gives 16 moves at best. We can have at most 6 squares to block an attack, so that's an additional 6 x 16 = 96 moves. So at best 8+16+96 = 120 moves, far less than 218, and thus we do not need to consider positions in which either king is in check.

So is this it Tobi? Can we now call NASA and ask for their supercomputer?

Nope, it's still absolutely hopeless, there are waaaaay too many positions left.
We have to skip even more positions.

Introducing Chess with Cheating: Partial Pieces and Moves

Reminder: Replace rook pictures by something more interesting.

While searching through all possible piece configurations, we would ideally like to have some provably correct way of telling whether we can still reach 218 moves, so we can stop trying and save ourselves an astronomically large amount of work. The better the method is, the more work we save. But it also needs to be fast, since we need to run it millions and billions of times.

A common technique in optimization is to allow fractional decisions. Instead of a piece being either on e4 or not, it can be 27.3% there and 72.7% not there. This enables us to just "swim" through the solution space towards the optimal solution instead of trying all combinations. The drawback is that we usually end up with a way too good solution with most decisions being fractional. But if that doesn't get us beyond 218 moves, we know we can stop trying.

Obviously, these kinds of algorithms are already implemented in state-of-the-art solvers like Gurobi, so all we need to do is model our problem to its likings (as a so-called integer programming problem), tell it to maximize the number of moves and pray. Finally, after ~55 000 seconds, it crashed.
Not enough memory, but also hopelessly far away from completing the proof. Extrapolating the runtime led to an estimated runtime of ~6 years. Yeah, let's not go there. Going back to making more observations:

Checking more positions to make things less slow

To reduce the size of the model, I bent some chess rules, simplifying the search space:

• I allowed castling if king and rook were on the right squares, not requiring anything else
• I stopped caring about pieces moving despite being pinned
• I stopped caring whether the white king is in check or walks into check
• I allowed white pawns to always capture when standing on the fifth rank so I'd not have to check en passant.

All of these things are unlikely to happen in 218+ move positions and after a solution has been found, I can still check and discard it if it has less moves than it claims to have.

I started again and this time, memory wasn't a problem, but the progress was awfully slow with ~29 days remaining. The world could not wait this long and neither could I. I pressed cancel.

Preventing white magic

The optimal fractional solution for the empty board. Most pieces are spread out over multiple squares and have fractional numbers of moves available that sum to ~305. This does prove that the real solution can't have more than 305 moves. Still quite a bit from proving 218 to be the optimum.

Our current way of cheating is too different from reality, causing the solver to have to search through way too many board configurations. In our case, the optimal solution to the easy problem flooded the center with half queens and half knights sharing the same squares, having half pieces move through other half pieces with half moves. Gurobi thinks that the above position has 305 moves in total, which is far away from 218 and a bad upper bound.

In order to cut off this crazy solution, I added a "redundant" constraint, saying that at most one piece in total can move from one direction onto a particular square. Which got us a new hallucination...

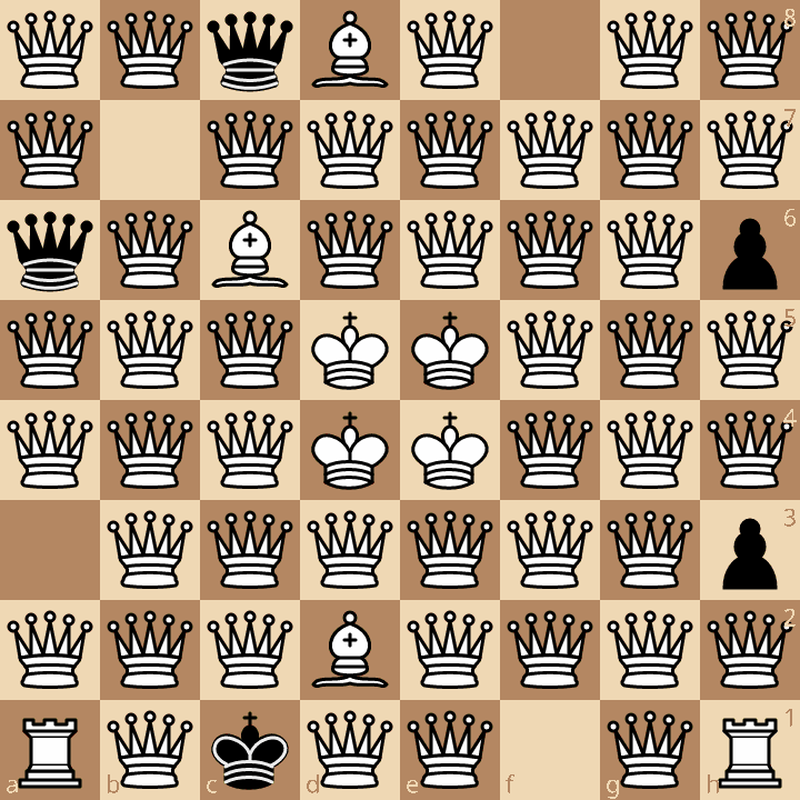
The second try. This one has 271 2/3 moves which proves that there is no solution with more than 271 moves.

Now we have 271 2/3 moves, which is much better. It's a bit like having to try all passwords with 53 characters vs. all passwords with 87 characters, the latter being many magnitudes harder.

Wait a minute, White can't have 4 kings.

White does not have four kings. White has 3 times 24.6% kings and one 26.2% king. Also, the queen on g3 barely exists, it's 0.8% but apparently it somehow contributes to the total sum of moves :)

With this improved model, I tried again and after ~23 000 seconds, Gurobi solved it to optimality!

Results

Sadly, instead of finding me a fancy position with 219 moves and making my name immortal, Gurobi gave me the following 12 representative positions (of 40,000 in total) with 218 moves each:

Link to the positions

All 12 positions seem trivially reachable. I only constructed a proof game for one of the positions, since that is sufficient for proving our claim. If you don't believe that this is possible, keep in mind that White's last or second last move might have been a capture. Or click on the link :)

Sadly not a world record, but at least we now know for certain that 218 is the limit.

And you smart chess move 3.7 bit compression people and chess engine developers, you can finally stop worrying. 256 moves will be enough. You're welcome :-)

Except if you allow non-reachable positions, in which case you might want to read on :P

Other stuff solved along the way

I also confirmed the optimality of the 144 move record without promotions. Since Gurobi did not find any position with more than 144 moves, that means that there also is no reachable position with more than 144 moves. Hence, 144 moves is the best we can do and "Jenő Bán", a chess composer from Hungary, found one in 1960 already:

144 moves for White, no promotions. Created by Hungarian chess composer "Jenő Bán". Here is a proof game, demonstrating that the position is reachable.

Also, I confirmed the optimality of the following illegal position, which has 288 moves for White.

Illegal position with 288 moves for White. Corner queens can be replaced with bishops.

Now have a guess at what the best non-reachable legal position looks like ;)
Yep, you're right, cramming the kings into the corners for 271 moves.

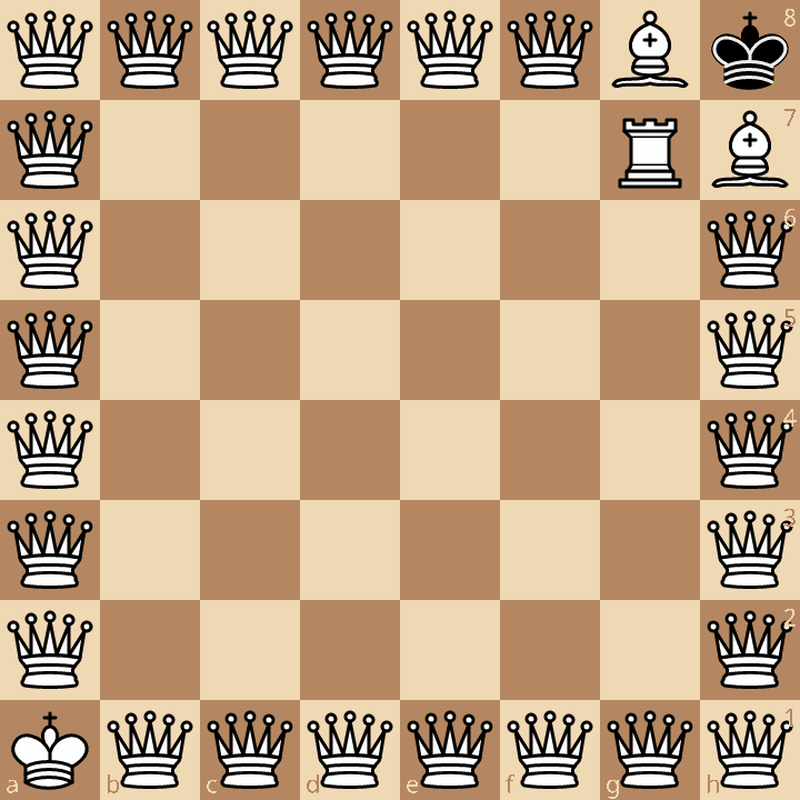
Legal but non-reachable position with 271 moves for White. Corner queens can be replaced with bishops.

Future plans

My code snippet is freely available at Github. If you manage to do something cool based on it, please let the world know :)

Fun problems enthusiasts could try to tackle next using similar techniques:

• Most captures
• Most stalemates
• Most checks
• Most checkmates
• Most mates in two
• ...
• Most ... under <condition>

Some of these might be hard, extremely hard or practically impossible to solve with current technology. I don't think that integer linear programming is a suitable approach for all of them, one likely has to develop a custom algorithm for computing good upper bounds, based on creative mathematical insights.

Good luck to those who dare to try solving one of these ^^